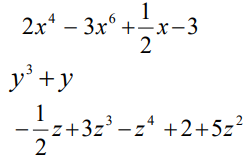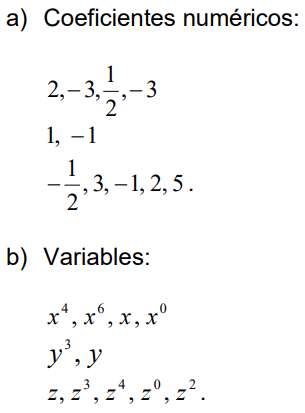Sobre Límites
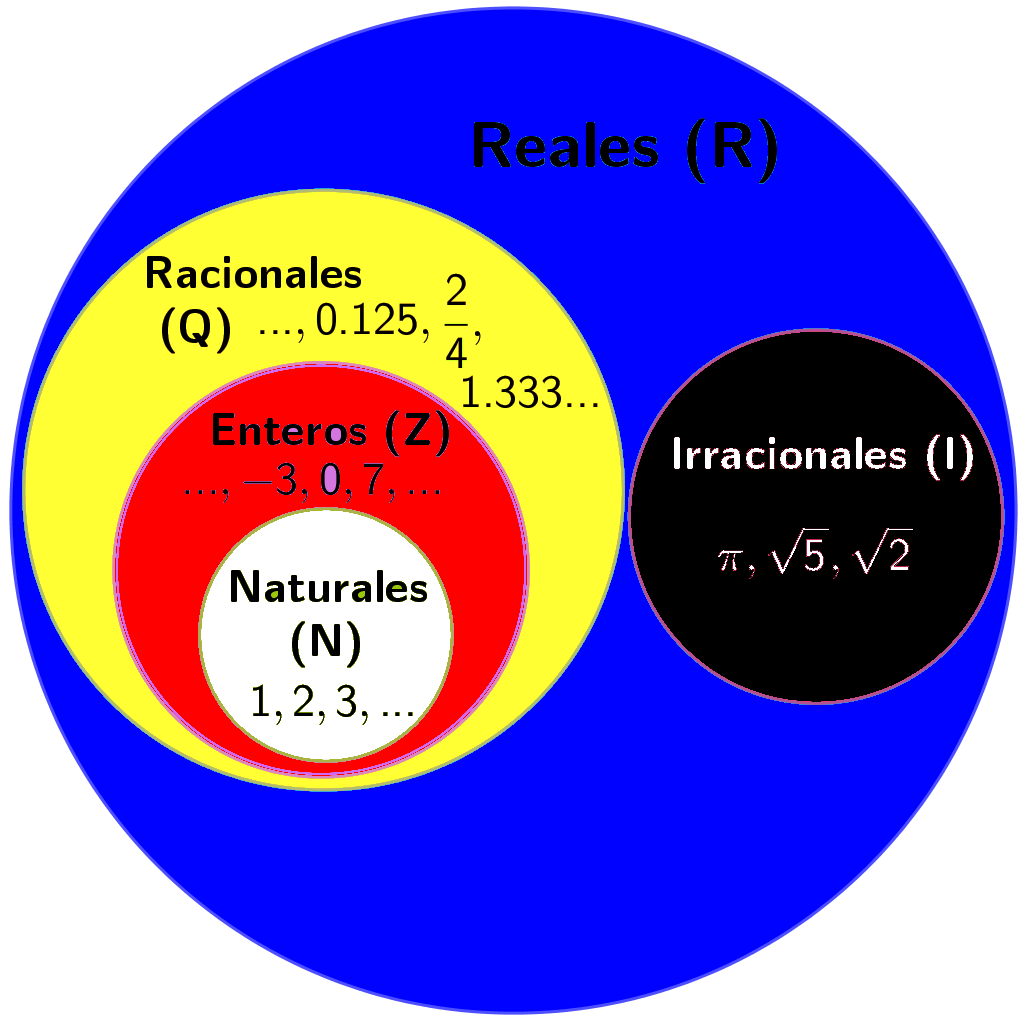
Los Numeros Naturales(N) son los enteros que representan existencias de lo que vemos, como 5 dedos, 2 ojos, 108 pétalos, etc, son números enteros positivos, pues en la naturaleza no hay fracciones ni negativos.
Los números enteros(Z), son los naturales y sus opuestos(los negativos) así como el cero(0).
en Los Números Racionales(Q), encontramos las fracciones, ya sean decimales o fraccionarias, positivas y negativas.
Los Números Irracionales(I) son aquellos que no representan una cantidad exacta, como se ejemplifica en la figura anterior.
Los Racionales(R) incluye a todos los anteriores
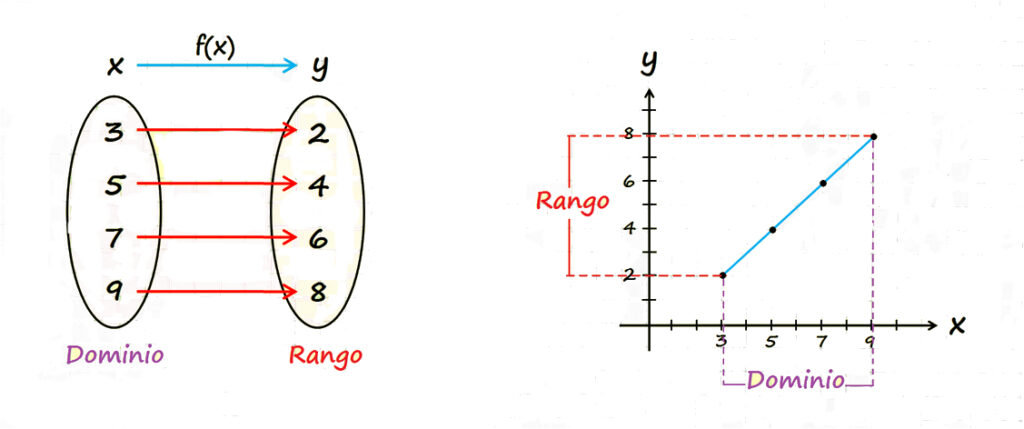
Ejercicios
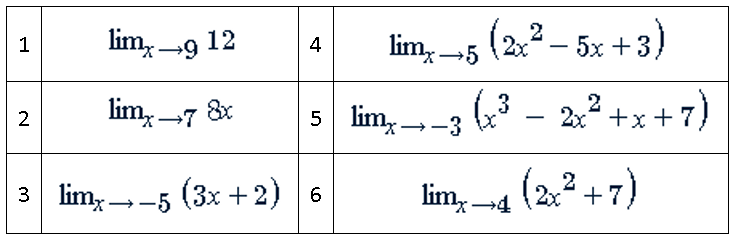
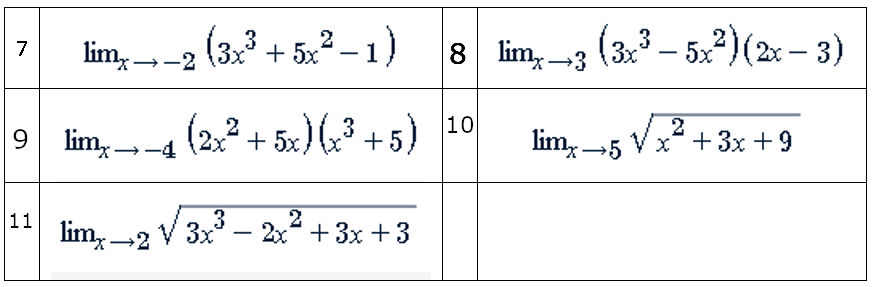
Metodologías de Desarrollo
La Metodología, (del griego metà “más allá”, odòs “camino” y logos “estudio”), hace referencia al conjunto de procedimientos basados en principios lógicos, utilizados para alcanzar una gama de objetivos que rigen en una investigación científica o en una exposición doctrinal.
(más…)Metodologías de investigación
Conceptos:
- Método: Son las formas de realizar una investigación de manera fácil; es el procedimiento que siguen las ciencias.
- Metodología: Es una herramienta de análisis lógico de los métodos de investigación.
Podemos definir a la metodología de la investigación como una disciplina que conjunta los procesos y técnicas que deben llevarse a cabo para realizar un estudio. Para presentar un proyecto realizado con esta metodología, es necesario utilizar formato APA; un estándar que permite distribuir y estructurar la información, así como hacer referencias y citar adecuadamente.
(más…)Mi instalación de Python
En windows…
Comenzamos descargando el instalador en la Página oficial

Vamos a descargas

Click en descargar:

Esperamos a que termine de descargar

Ejecutamos el archivo descargado y nos ejecuta el asistente, solo seguir las instrucciones hasta concluir, nada diferente a la instalación de cualquier aplicación de win2.

Y concluye la instalación:

Una vez instalado, el IDLE siempre lo anclo en el inicio:

Y pues nada, solo ejecutamos el IDLE y tenemos nuestra terminal lista para programar

Proceso de Diseño Creativo
Se propone la siguiente definición de creatividad:
La capacidad de producir cosas nuevas y valiosas.
La palabra cosas se toma en el sentido más amplio, que incluye prácticamente todo.
En términos generales podemos distinguir tres grados o niveles para valorar el producto:
- El producto es valioso para el círculo afectivo del sujeto creador.
- Es valioso para su medio social.
- Es valioso para la humanidad.
Resultan así tres niveles de creación, que podríamos llamar:
- El nivel elemental o de interés personal y familiar.
- El nivel medio o de resonancia laboral y profesional.
- El nivel superior o de la creación trascendente y universal.
Estadística inferencial
En Estadística se le llama Inferencia al Proceso de Inducir o Deducir las características o parámetros poblacionales a partir de la información muestral, midiendo con probabilidades la incertidumbre inherente.
Lo anterior se puede realizar ya sea como un valor puntual, como un intervalo, o bien, establecer valores hipotéticos de los parámetros y probar estadísticamente si son válidas las hipótesis. A los primeros dos casos se les conoce como Estimación estadística puntual o por intervalos y a los segundos, Prueba de hipótesis.
(más…)Herramientas para la ejecución de pruebas
Las pruebas de software automatizadas son una nueva tendencia en la ingeniería de software. Es una tecnología que permite completar los procedimientos de prueba con poca o ninguna interacción humana del diseño de la prueba inicial hasta la ejecución de la prueba final.
Esta tecnología beneficia el proceso de prueba al aumentar su eficiencia y repetibilidad, reducir el error humano y aumentar la profundidad a la que se realiza el análisis de los resultados.
(más…)Derivadas parciales
La introducción de las derivadas parciales ocurrió años después del trabajo sobre el cálculo de Newton y Leibniz. Entre 1730 y 1760, Leonhard Euler y Jean Le Rond d’Alembert publicaron por separado varios artículos sobre dinámica en los cuales establecieron gran parte de la teoría de las derivadas parciales. Estos artículos utilizaban funciones de dos o más variables para estudiar problemas de equilibrio, movimiento de fluidos y cuerdas vibrantes.
Por ejemplo, para determinar el efecto de un catalizador en un experimento, un químico podría repetir el experimento varias veces usando cantidades distintas de catalizador, mientras mantiene constantes las otras variables como temperatura y presión. Para determinar la velocidad o la razón de cambio de una función f respecto a una de sus variables independientes se puede utilizar un procedimiento similar. A este proceso se le llama derivación parcial y el resultado se llama derivada parcial de f con respecto a la variable independiente elegida.
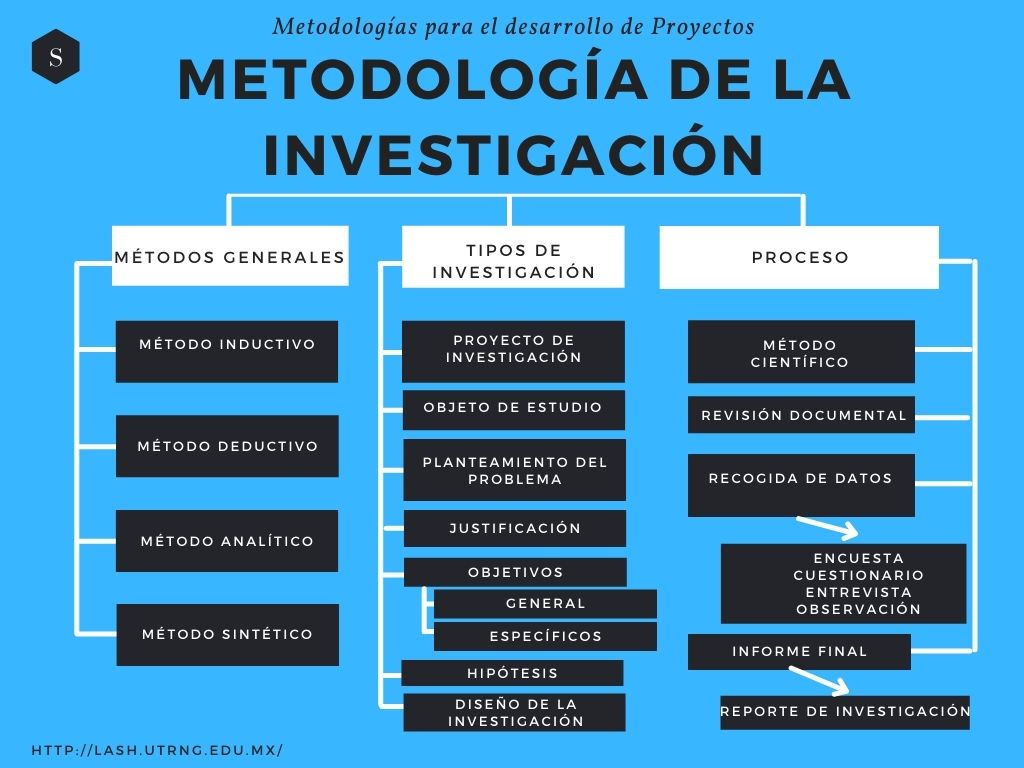
(más…)Operaciones Algebraicas de Polinomios
Los polinomios se construyen mediante la aplicación repetida de las operaciones elementales de: Potencias, Multiplicaciones, Divisiones, adiciones y restas, P. ej:
A cada expresión se le llama “términos algebraicos” e indican sumas o restas de monomios, las cuales forman Polinomios, van separadas por los signos “+” y “-“, se forman por constantes y variables. Ejemplo:
(más…)Pruebas de software
Aunque pueda resultar paradójico, el principal objetivo de las pruebas debe ser conseguir que el programa funcione incorrectamente y que se descubran sus defectos.
Las pruebas no permiten garantizar la calidad de un producto. Puede decirse que una prueba tiene éxito si se descubre algún error, con lo que se sabe que el producto no cumple con algún criterio de calidad; por el contrario, si la prueba no descubre ningún error, no se garantiza con ello la calidad del producto, ya que pueden existir otros errores que habrían de descubrirse mediante pruebas diferentes.
(más…)