Inicio » SegundoParcialProbabilidadParamed
Archivos de la categoría: SegundoParcialProbabilidadParamed
Ejercicios de Distribución de Poisson
Ejercicio 1
El recuento de leucocitos de un individuo sano puede presentar en promedio un valor mínimo de hasta 6000 por mm3 de sangre. Para detectar una deficiencia de leucocitos, se toma una gota de sangre de 0.001 mm3 y se halla el número X de leucocitos.
¿Cuántos leucocitos cabe esperar en un individuo sano? Si a lo sumo se encuentran dos, ¿hay signos de una deficiencia de leucocitos? Este experimento puede considerarse un proceso de Poisson. El suceso discreto de interés es encontrar un leucocito, el intervalo continuo es una gota de sangre. Sea el mm3 la unidad de medida; así, s = 0.001 y λ, la media de veces que tendremos un suceso por cada unidad, es 6000. Por lo tanto, X es una variable aleatoria de Poisson con P[X] = λ = 6000(0.001) = 6. Para una persona con buena salud, esperaríamos observar un promedio de, por lo menos, seis leucocitos. ¿Sería extraño encontrar dos células como máximo? ¿Lo expresaremos por P[ X ≤ 2 | λ = 6 ] ? R= 0.062
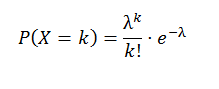
Ejercicio 2
En el estudio del sueño en los seres humanos se reconocen cinco fases (somnolencia, ligero, intermedio, profundo, REM) por medio del electroencefalograma. El sueño intermedio se caracteriza por la presencia de ondas de gran amplitud, que aparecen en un promedio de alrededor de dos ondas por segundo.
- ¿Cuál es la probabilidad de que, durante un sueño intermedio, no se presente ninguna de estas ondas durante un período de cinco segundos?
- ¿Cuál es la probabilidad de que aparezca un máximo de 15 de tales
- ondas en un período de cinco segundos?
- Si aparecieran 20 ó más de tales ondas durante un período de cinco segundos, ¿podría sospecharse que el sujeto no está en la etapa de sueño intermedio? Razonar sobre la base de la probabilidad implícita.
Instrucciones de entrega
Resolver en cualquier medio que les sea más cómodo(cuaderno, hoja blanca, word, excel, etc), en caso de hacerlo físicamente en hojas blancas o cuaderno, fotografiar o escanear.
Una vez resueltos los ejercicios, crear una carpeta con sus datos y comprimirla en rar o zip. P. ej.
Enviar al correo lsaucedoh@utrng.edu.mx
Ejercicios de Distribución Binomial
Ejercicio 1
Se va a construir una planta nuclear y se quiere conocer la opinión de los vecinos de la localidad. Se selecciona una muestra aleatoria de 20 individuos y se realiza un sondeo. Se piensa que el 60 % de los habitantes del lugar estará a favor del proyecto. Si esto es verdad, ¿cuántos piensa usted que expresarían una opinión favorable? Si sólo nueve o menos son de tal opinión, ¿piensa usted que es razón de peso para poner en duda la cifra 60 %? Explicarlo sobre la base de la probabilidad implícita.
Ejercicio 2
Para estudiar la regulación hormonal de una línea metabólica, se inyecta a ratas albinas un fármaco que inhibe la síntesis de proteínas del organismo. En general, 4 de cada 20 ratas mueren a causa del fármaco antes de que el experimento haya concluido. Si se trata a 10 animales con el fármaco, ¿cuál es la probabilidad de que al menos 8 lleguen vivos al final del experimento?
Instrucciones de entrega
Resolver en cualquier medio que les sea más cómodo(cuaderno, hoja blanca, word, excel, etc), en caso de hacerlo físicamente en hojas blancas o cuaderno, fotografiar o escanear.
Una vez resueltos los ejercicios, crear una carpeta con sus datos y comprimirla en rar o zip. P. ej.
Enviar al correo lsaucedoh@utrng.edu.mx
Distribución de Poissón
Es una distribución de variable discreta, Los sucesos son independientes y ocurren durante un intervalo de tiempo dado ( segundos , minutos , horas, etc) o en una región específica
Ejemplos
- El número de coches que pasan a través de un cierto punto en una carretera
- El número de errores de ortografía que uno comete al escribir en una página
- El número de llamadas telefónicas en una central telefónica por minuto ( día , hora, etc)
- El número de enfermos que llegan por hora (Día , mes) a un hospital
- El número de clientes que llegan a una oficina por hora (Día , semana)
- El número de defectos por metro cuadrado de tela.
- El número de estrellas en un determinado volumen de espacio.
Distribución Binomial
Un experimento sigue el modelo de la distribución binomial o de Bernoulli si:
1. En cada prueba del experimento sólo son posibles dos resultados: el suceso A (éxito) y su contrario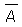
2. La probabilidad del suceso A es constante, es decir, que no varía de una prueba a otra. Se representa por p.
(más…)Concepto de Probabilidad
Se define como cálculo de probabilidad al conjunto de reglas que permiten determinar si un fenómeno ha de producirse, fundando la suposición en el cálculo, las estadísticas o la teoría. La probabilidad es la parte de las matemáticas que trata de manejar con números la incertidumbre.
El valor más pequeño que puede tener la probabilidad de ocurrencia de un evento es igual a 0, el cual indica que el evento es imposible, y el valor mayor es 1, que indica que el evento ciertamente ocurrirá.
0 ≤ P(A) ≤ 1
y así tenemos que P(A)+ P(A’ )=1
(más…)
