Inicio » SegundoParcialProb-Mecatro
Archivos de la categoría: SegundoParcialProb-Mecatro
Ejercicios del Teorema de Bayes
Ejercicio 1.
Supongamos que en una determinada población se conoce de antemano que el 5% padecen diabetes tipo II. A través de una muestra, en la cual la mitad de los pacientes eran diabéticos y la otra mitad no, se estimó mediante la tabla de contingencia que la proporción de hipertensos era de un 60% entre los diabéticos y de un 15% entre los no diabéticos. Comprobar los resultados propuestos:
- (a) Estima la proporción de hipertensos en la población. R = 37.5%
- (b) Estima también la proporción de hipertensos que son diabéticos. R= 30%
- (c) Estima la proporción de diabéticos entre los hipertensos y compárala con la proporción de diabéticos entre los no hipertensos. R = 30% vs 20% o 6 de cada 10 diabéticos son Hipertensos
- (d) Representa las cuatro posibilidades del estudio mediante un diagrama de Venn.
Ejercicio 2.
Se cree que la distribución de los grupos sanguíneos en Estados Unidos en
la Segunda Guerra Mundial era: tipo A, 41 %; tipo B, 9 %; tipo AB, 4 %; y tipo 0,46 %. Se estima que en esa época, el 4 % de las personas pertenecientes al tipo 0 fue clasificado como del tipo A; el 88 % de los del tipo A fue correctamente clasificado; el 4 % de los del tipo B se clasificó como del tipo A, y el 10 % de los del tipo AB fue, igualmente, clasificado como del tipo A. Un soldado fue herido y conducido a la enfermería. Se le clasificó como del tipo A. ¿Cuál es la probabilidad de que tal grupo sea ciertamente el suyo?
A1: Es del tipo A.
A2: Es del tipo B.
A3: Es del tipo AB.
A4: Es del tipo 0.
B: Es clasificado como del tipo A.
Ejercicio 3
Las estadísticas indican que en Estados Unidos la probabilidad de que una madre muera durante el parto es 0.00022. Si no es de raza negra, la probabilidad de muerte es 0.00017, mientras que si lo es, esta probabilidad aumenta a 0.00064. Supongamos que el 10 % de los partos corresponde a mujeres negras.
- Dibujar un diagrama de árbol describiendo las probabilidades dadas, y hallar las probabilidades correspondientes a las trayectorias en cada uno de los cuatro casos. (Sea D el suceso que denota que la madre muere y B el que alude a que es de raza negra.)
- Utilizar el árbol del inciso a) para calcular la probabilidad de que una madre que muere en el parto sea de raza negra.
- Haciendo uso del teorema de Bayes, hallar la probabilidad de que una madre que muere en el parto sea de raza negra, y comparar el resultado con el obtenido en el inciso b).
Ejercicio 4
Un test diseñado para diagnosticar el cáncer de cuello uterino tiene un coeficiente de falsos negativos y falsos positivos de 0.05, cada uno. De una cierta población de mujeres, el 4 % está afectado por este tipo de cáncer. ¿Cuál es la probabilidad de que una mujer de la población elegida aleatoriamente tenga cáncer de cuello uterino, dado que su resultado
con el test es positivo?
Instrucciones de entrega
Resolver en cualquier medio que les sea más cómodo(cuaderno, hoja blanca, word, excel, etc), en caso de hacerlo físicamente en hojas blancas o cuaderno, fotografiar o escanear.
Una vez resueltos los ejercicios, crear una carpeta con sus datos y comprimirla en rar o zip. P. ej.
Enviar al correo lsaucedoh@utrng.edu.mx
Teorema de Bayes
El teorema de Bayes es utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso. Eventos mutuamente excluyentes.
Si A1, A2, … , Anson:
Sucesos incompatibles 2 a 2.
Y cuya unión es el espacio muestral (A 1 ∪ A 2 ∪… ∪ A n = E).
Y B es otro suceso.
Resulta que:
Para calcular la probabilidad tal como la definió Bayes en este tipo de sucesos, necesitamos una fórmula. La fórmula se define matemáticamente como:
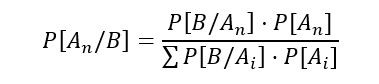
Donde B es el suceso sobre el que tenemos información previa y A(n) son los distintos sucesos condicionados. En la parte del numerador tenemos la probabilidad condicionada, y en la parte de abajo la probabilidad total. En cualquier caso, aunque la fórmula parezca un poco abstracta, es muy sencilla
o
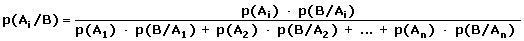
Las probabilidades p(A1) se denominan probabilidades a priori.
Las probabilidades p(Ai/B) se denominan probabilidades a posteriori.
Las probabilidades p(B/Ai) se denominan verosimilitudes.
(más…)
Concepto de Probabilidad
Se define como cálculo de probabilidad al conjunto de reglas que permiten determinar si un fenómeno ha de producirse, fundando la suposición en el cálculo, las estadísticas o la teoría. La probabilidad es la parte de las matemáticas que trata de manejar con números la incertidumbre.
El valor más pequeño que puede tener la probabilidad de ocurrencia de un evento es igual a 0, el cual indica que el evento es imposible, y el valor mayor es 1, que indica que el evento ciertamente ocurrirá.
0 ≤ P(A) ≤ 1
y así tenemos que P(A)+ P(A’ )=1
(más…)
