Cuando la luz incide sobre la superficie de un objeto, parte de la luz se refleja. El resto puede ser absorbido por el objeto (y transformarse en energía térmica) o, si el objeto es transparente como el vidrio o el agua, una parte se transmite a través de él. En el caso de un objeto muy liso y brillante, como un espejo plateado, se refleja más del 95% de la luz.
Cuando un estrecho haz de luz incide sobre una superficie plana, se define el ángulo de incidencia,θi, como el ángulo que un rayo incidente forma con la normal (perpendicular) a la superficie, y el ángulo de reflexión, θr , como el ángulo que el rayo reflejado forma con la normal. Se encuentra que los rayos incidente y reflejado están en el mismo plano con la normal a la superficie y que:
el ángulo de reflexión es igual al ángulo de incidencia, θi=θr
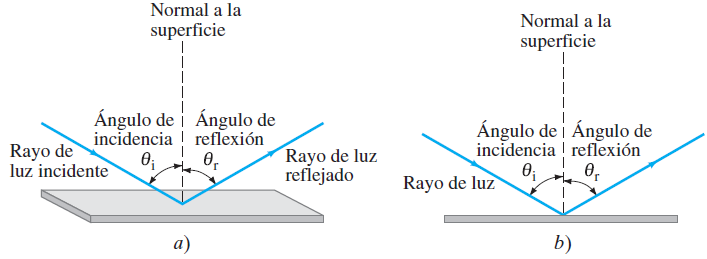
a) Vista tridimensional de un rayo incidente reflejado en lo alto de una superficie plana;
b) vista lateral o “desde el extremo”, que se usará normalmente en virtud de su claridad.
Cuando la luz incide sobre una superficie rugosa, incluso microscópicamente rugosa, la luz se refleja en muchas direcciones, a esto se le llama reflexión difusa. Sin embargo, aún se sostiene la ley de reflexión en cada pequeña sección de la superficie. Gracias a la reflexión difusa en todas direcciones, un objeto ordinario se puede ver en muchos ángulos diferentes por la luz que se refleja en él. Cuando uno mueve la cabeza hacia un lado, diferentes rayos reflejados alcanzan nuestros ojos desde cada punto del objeto,
Comparemos la reflexión difusa con la reflexión en un espejo, lo que se conoce como reflexión especular. (“Speculum” en latín significa espejo.) Cuando un estrecho haz de luz brilla en un espejo, la luz no llegará a nuestros ojos a menos que éstos se ubiquen justo en el lugar correcto donde se satisfaga la ley de reflexión,
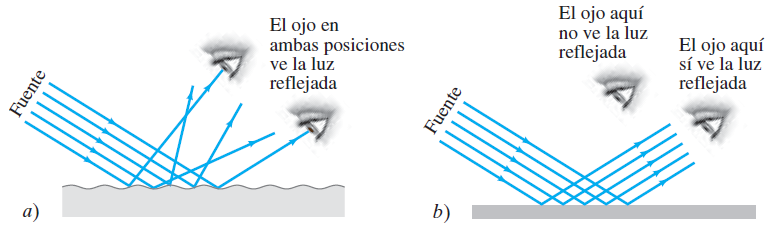
En el inciso a) usted puede ver con su ojo la luz blanca reflejada en varias posiciones debido a la reflexión difusa.
Pero en el inciso b) usted ve la luz reflejada sólo cuando sus ojos se ubican en el lugar
correcto (θi=θr);
Ejemplo 1:
Reflexión en espejos planos. Dos espejos planos son perpendiculares
entre sí. Un haz de luz entrante forma un ángulo de 15º con el primer espejo, como se muestra en la figura izquierda. ¿Qué ángulo formará el haz saliente con el segundo espejo?
PLANTEAMIENTO Bosqueje la trayectoria del haz conforme se refleja en los dos espejos y dibuje las dos normales a los espejos para las dos reflexiones. Use geometría y la ley de reflexión para encontrar los diversos ángulos.
Solución: θ1 +15° =90, de manera que θ1=75°, por ley de Reflexión, θ2=θ1=75° también. Las dos normales a los espejos son perpendiculares entre sí, de manera que θ2 + θ3 + 90° = 180°, como sucede con cualquier triángulo. Por ende, θ3 = 180° – 90° – 75°, = 15°. Por ley de Reflexión, θ4 = θ3 = 15°, es el ángulo que el rayo reflejado forma con la superficie del segundo espejo(Figura de la derecha).
NOTA : El rayo saliente es paralelo al rayo entrante. Los reflectores rojos de las bicicletas y de los automóviles se basan en este principio.
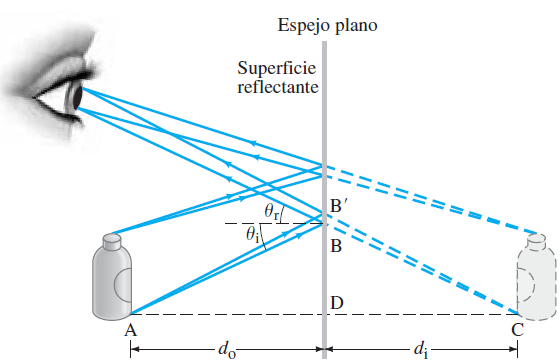
Un espejo “plano” es aquél con una suave superficie reflectora plana. A continuación se muestran los rayos provenientes de dos puntos diferentes
de un objeto (la botella a la izquierda en la figura): se ilustran dos rayos
que salen de un punto en la parte superior de la botella, y dos más desde un punto en la parte inferior. Los rayos que salen de cada punto en el objeto van en muchas direcciones, pero sólo se muestran aquellos que encierra el haz de rayos que entra al ojo y que provienen de cada uno de los dos puntos. Cada conjunto de rayos divergentes que se reflejan
en el espejo y entran al ojo parecen provenir de un solo punto (llamado punto de imagen) detrás del espejo, como se indica mediante las líneas punteadas. Esto es, los ojos y el cerebro interpretan que cualquier rayo que entra al ojo viajó en trayectoria de línea recta. El punto desde donde parece provenir cada haz de rayos es un punto en la imagen. Para cada punto en el objeto, existe un punto de imagen correspondiente.
Ejemplo 2:
¿De qué altura debe ser un espejo de cuerpo completo? Una mujer de 1.60 m de altura está de pie frente a un espejo plano vertical. ¿Cuál es la altura mínima del espejo, y qué tan cerca del suelo debe estar su borde inferior, si ella desea ver todo su cuerpo? Suponga que los ojos de la mujer están situados 10 cm por debajo de la parte superior de su cabeza.
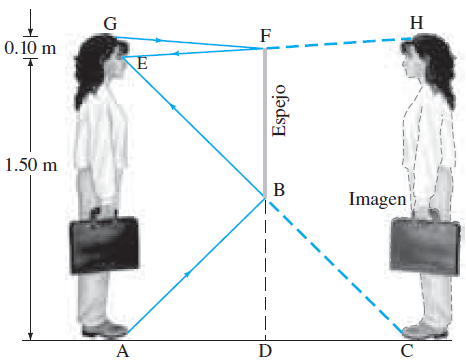
PLANTEAMIENTO: Para que ella vea todo su cuerpo, los rayos de luz provenientes de la parte superior de su cabeza y de la punta de sus pies deben reflejarse en el espejo y entrar a sus ojos; véase la figura abajo. No se muestran dos rayos divergentes desde cada punto como se hizo en la figura de la botella, donde se quería encontrar dónde estaba la
imagen. Ahora que se sabe que la imagen está a la misma distancia detrás de un espejo plano como lo está el objeto enfrente de él, sólo se necesita dibujar un rayo que salga del punto G (parte superior de la cabeza) y un rayo que salga del punto A (los dedos de sus pies) y luego usar geometría simple.
SOLUCIÓN: Primero considere el rayo que sale de los pies de la mujer en A, se refleja en B y entra al ojo en E. El espejo no necesita extenderse más abajo de B. Puesto que el ángulo de reflexión es igual al ángulo de incidencia, la altura BD es la mitad de la altura AE.
Dado que AE = 1.60 m – 0.10 m = 1.50 m, entonces BD = 0.75 m. De igual modo, si la mujer debe ver la parte superior de su cabeza, el borde superior del espejo sólo necesita alcanzar el punto F, que está 5 cm abajo de la parte superior de su cabeza (la mitad de GE = 10 cm). Por lo tanto, DF= 1.55 m y el espejo necesita tener una altura vertical de sólo (1.55 m – 0.75 m) = 0.80 m. El borde inferior del espejo debe estar a 0.75 m sobre el suelo.
NOTA Se concluye que un espejo, si se coloca bien, sólo necesita medir la mitad de la altura de una persona para que ésta se vea por completo.
Ejercicio
Suponga que está de pie a 3 m enfrente de un espejo en una estética. Puede verse usted mismo desde su cabeza hasta la cintura, pues el borde inferior del espejo corta el resto de su imagen. Si se acerca más al espejo:
- no podrá ver más de su imagen;
- podrá ver más de su imagen, abajo de su cintura;
- verá menos de su imagen, y el corte se elevará para estar arriba de su cintura.
Explique
Ejercicios:
Dibujar el esquema de la trayectoria del rayo de luz y determinar el Ángulo de salida que se pide.
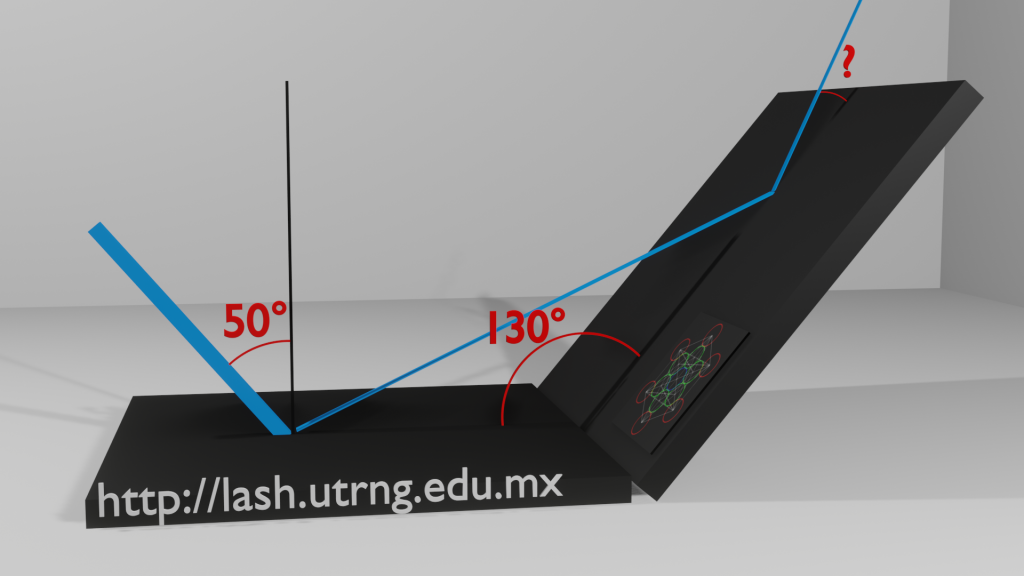
Ejercicio 1. Un rayo de luz incide sobre un espejo horizontal formando un ángulo de 50º con la normal. Sabiendo que a la derecha de dicho espejo se sitúa otro con el que forma un ángulo de 130º, determina la dirección del rayo después de reflejarse en este segundo espejo.(Ver figura 1)
Ejercicio 2. Un rayo de luz incide sobre un espejo horizontal formando un ángulo de 45º con la normal(linea negra). Sabiendo que el espejo a la derecha forma un ángulo de 95º, determina la dirección del rayo después de reflejarse en este segundo espejo.(Ver figura 2)
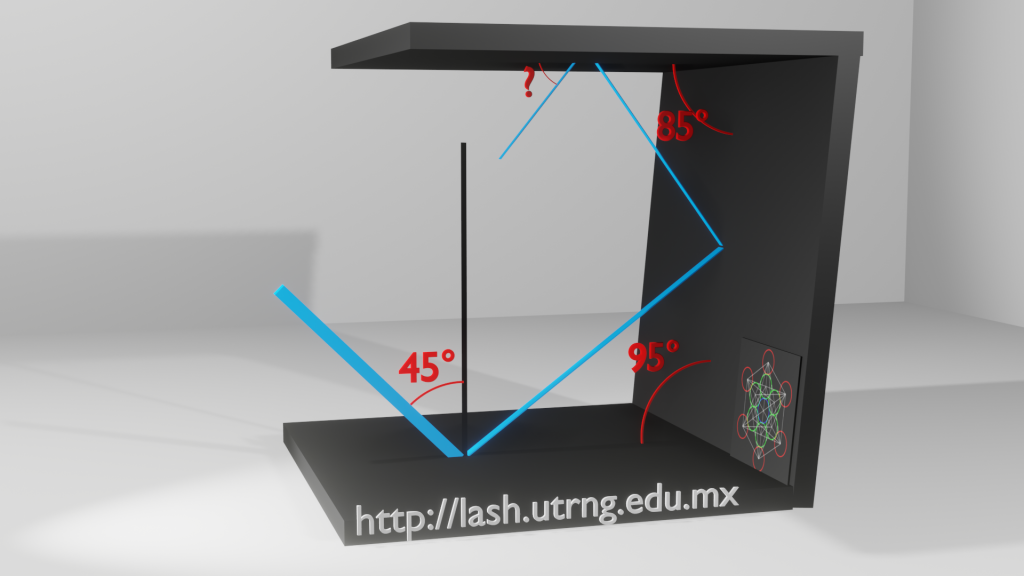
Ejercicio 3. En esta ocasión, el rayo de luz incide sobre tres espejos, el primero, un espejo horizontal, forma un ángulo de 45º con la normal(rayo y linea negra). El primer espejo con el segundo, forma un ángulo de 95º, y éste último con el tercero, forman un ángulo de 85°, determina la dirección del rayo después de reflejarse en éste último espejo.(Ver figura 3).



Muy buenas las explicaciones gracias