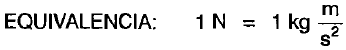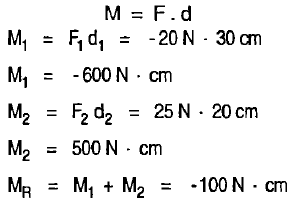La Estática es una parte de la Mecánica que estudia el equilibrio mecánico de los cuerpos.

El Equilibrio mecánico

Es aquel estado en el cual un cuerpo mantiene su velocidad constante(cte); existen dos tipos de equilibrio: Estático y Cinético.

Si el cuerpo se encuentra en reposo: ¡Hay Equilibrio Estático!

V = cte = 0

Si el cuerpo se encuentra en movimiento rectilíneo uniforme:¡Existe Equilibrio cinético!

V = cte

V = cte > 0

Fuerza  F

Es una magnitud vectorial que mide el grado de intensidad de una interacción. Llamaremos interacción a la influencia mutua de dos cuerpos en contacto o a distancia. La fuerza puede originar en los cuerpos, entre otros efectos los siguientes: cambios en su velocidad, cambios en sus dimensiones y también puede originar giros o rotaciones (cuplas), en los cuerpos rígidos (no deformables).

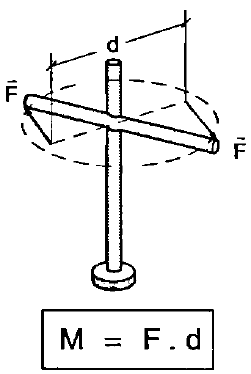
Cupla

Se llama así a un par de fuerzas de igual módulo y dirección contraria, aplicadas a un mismo cuerpo. Su valor se calcula en forma similar al del momento de una fuerza. NOTA: La Cupla no es sino un Momento.

Unidades del SI: N y m.

• M: Momento de la Cupla en N.m
• F: Valor de cada una de las fuerzas iguales en N
• d: Distancia entre las dos Fuerzas en m

RESULTANTE del Sistema de Fuerzas

Se llama resultante de un sistema de fuerzas que actúan sobre un cuerpo a una fuerza que los reemplace, produciendo sobre el cuerpo el mismo efecto que el sistema.

1  Resultante de fuerzas que tienen la misma línea de acción y sentidos opuestos:

• Su recta de acción es la misma que la de los componentes.
• Su medida es la diferencia de las componentes.
• Su sentido es el del que tiene mayor valor absoluto.
• Su punto de aplicación es cualquier punto de la línea de acción.

• El equilibrio se consigue aplicando una fuerza igual y contraria a la resultante.

2  La resultante de cuplas con respecto a un mismo eje:

• Su dirección: la de su eje de rotación.
• Su sentido: Se determina por la regla de la mano derecha o “tirabuzón”.
• Su medida: La medida de su momento “F . d”.
• Su punto de aplicación: Es cualquiera, es un vector libre.
• El equilibrio se consigue aplicando una cupla igual y contraria a la resultante.

NOTA: La unidad del SI de la Fuerza es el Newton(N). Es la Fuerza que al aplicar un Kg de masa, se le ocasiona una aceleración 1 m/s²

Ejemplo 1.

Una persona empuja una puerta hacia afuera con una fuerza de 20 N y a una distancia de 30 cm de la bisagra. Otra empuja hacia adentro con una fuerza de 25 N y a 20 cm de la bisagra eje. hallar la resultante.

Llamando (+) y (-) los sentidos de las fuerzas, tenemos

3  La resultante de fuerzas con la misma línea de acción y el mismo sentido:

• Su recta de acción, es la misma que la de los componentes.
• Su sentido, el mismo que los componentes.
• Su medida es la suma.
• Su punto de aplicación es cualquier punto de la recta de acción.

4  Resultante de fuerzas concurrentes:

• Dos o más fuerzas son concurrentes cuando sus rectas de acción se cortan en un punto. La resultante se halla por el método del polígono de fuerzas, por el método del paralelogramo o por el sistema de ejes cartesianos.

Ejemplo 2.

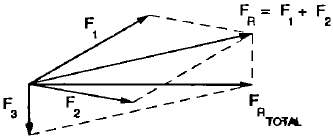
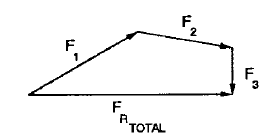
Sean las Fuerzas F₁ F₂ y F₃, que se cortan en el punto 0, Hallar gráficamente la resultante.

Resolución

Método del paralelogramo

Método del polígono de fuerzas

Ejemplo 3

Mediante un lazo, jalan un carro dos personas con fuerzas de 30N y 40N, haciendo un ángulo de 120°. Calcular la Resultante y la Dirección que seguirá el automóvil al moverse. las fuerzas son coplanares.

Resolución

Calculamos el módulo de fuerza resultante mediante la ley del paralelogramo:

De la ley de Senos se tiene:

5  Resultante de fuerzas paralelas y del mismo sentido:

• Su recta de acción es paralela a las fuerzas.
• Su sentido, el de las fuerzas.
• Su medida, la suma.
• Su punto de aplicación está situado en un punto que divide a la barra que une las fuerzas en segmentos inversamente proporcional a las fuerzas (Ley de Stevin).

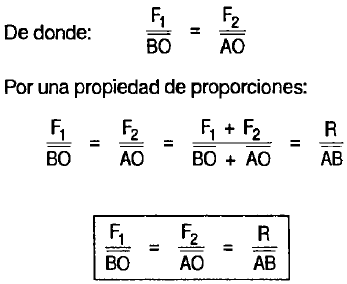
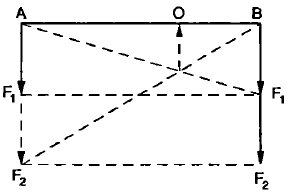
Relación de Stevin

Sea O el punto de aplicación de la Resultante por Momentos:

F₁ x AO = F₂ x BO

De la expresión se despeja AO o BO según cual de los extremos de la barra se quiera tomar como referencia.

Ejemplo 4.

Un cuerpo soporta la acción de dos fuerzas paralelas, y del mismo sentido F₁ = 16 N , y F₂ = 30 N; la distancia que los separa es de 1.20 m. Calcular:

• a) La resultante.
• b) El punto de aplicación.

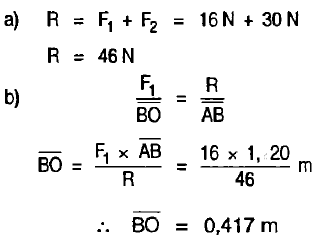
Método gráfico para hallar el punto de aplicación para la resultante

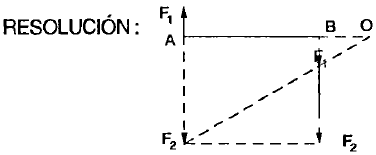
6  Resultante de fuerzas paralelas y de sentido contrario:

• Su recta de acción es paralela a las fuerzas.
• Su sentido, es el de fuerza mayor.
• Su medida, la diferencia.
• Su punto de aplicación, está situado en un punto que divide a la barra que une las fuerzas en segmentos, inversamente proporcionales a las fuerzas (Ley de Stevin).

Ejemplo 5.

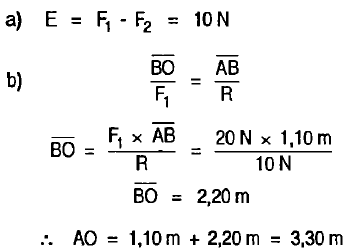
Sean los módulos de dos fuerzas F =20N F = 30N dirigidas en sentido contrario y paralelas separadas en 1.10 m, Calcular:

• a) El módulo Resultante.
• b) El punto de aplicación