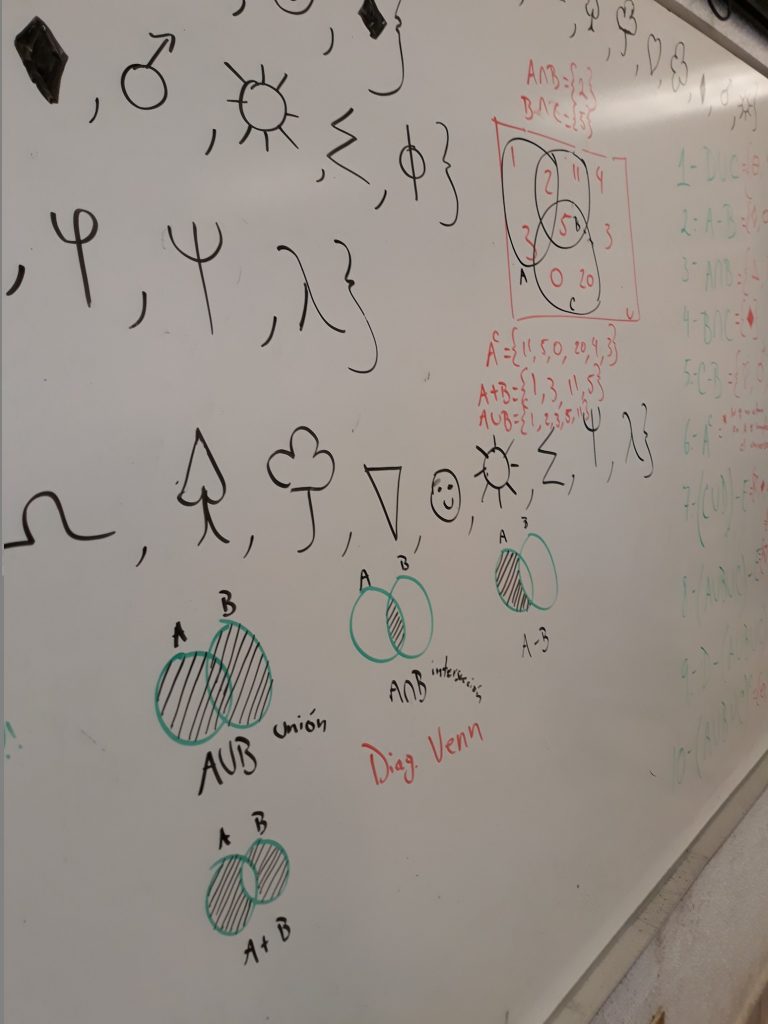Antiderivada / Integral Indefinida
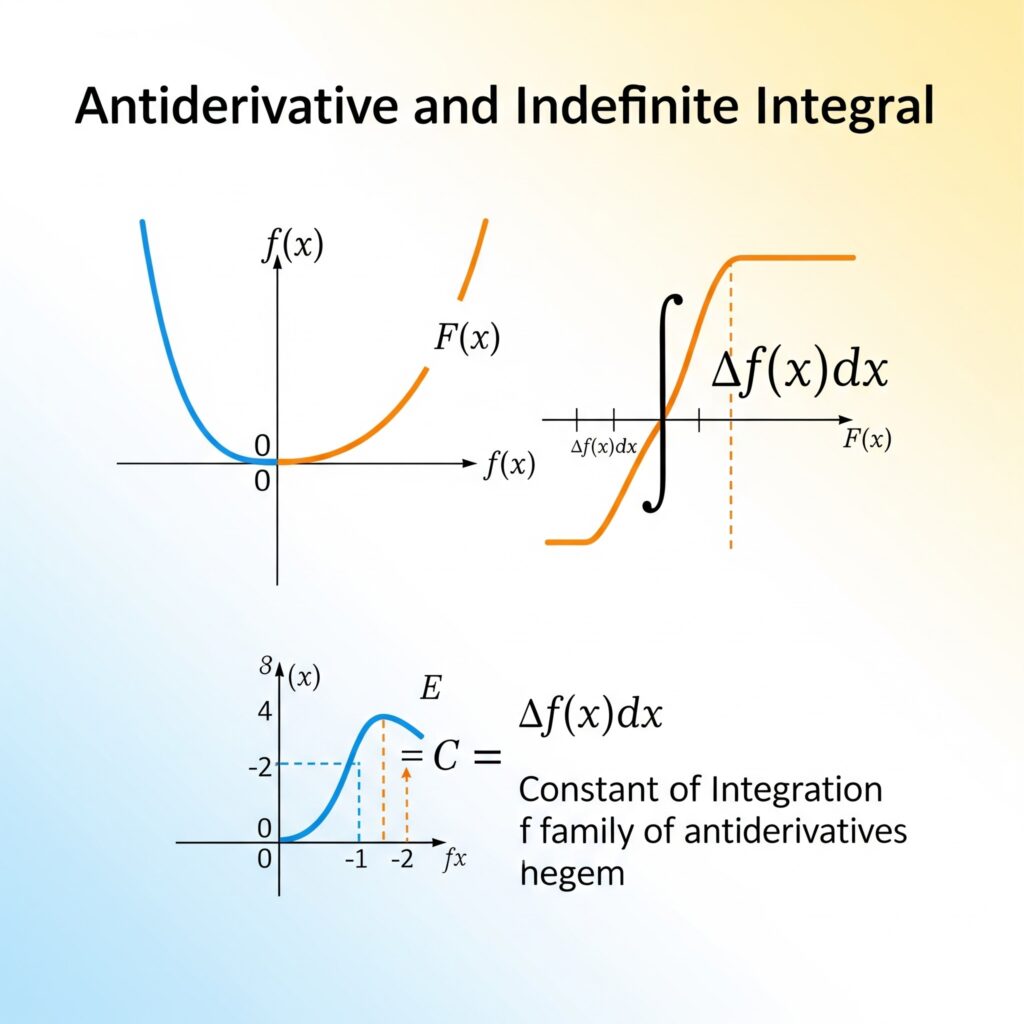
Antiderivadas
La mayoría de las operaciones matemáticas con que trabajamos vienen en pares de inversas: suma y resta, multiplicación y división, y exponenciación y extracción de raíces. Una razón de operaciones inversas es su utilidad en la resolución de ecuaciones. Por ejemplo, la resolución de x3 = 8, esto implica el uso de extraer raíces.
Si queremos resolver ecuaciones que incluyan derivadas necesitaremos su inversa, denominada antiderivación o integración.
Definición(click Expandir/contraer)
Llamamos a F una antiderivada de f en el intervalo I si DxF(x) = f (x) en I; esto es, si F'(x) = f (x) para toda x en I.
Ejemplo
1. Encuentre una antiderivada de la función f (x) = 4x3 en (- ∞,∞).
SOLUCIÓN: Buscamos una función F que satisfaga F'(x) = 4x3 para toda x real.
La función F(x) = x4 + 6 también satisface F'(x) = 4x3; también es una antiderivada de f (x) = 4x3.
De hecho, F(x) = x4 + C, donde C es cualquier constante, es una antiderivada de 4x3 en (- ∞,∞)
2. Encuentre la antiderivada general de f (x) = x2 en (- ∞,∞).
SOLUCIÓN: la antiderivada general es 
Regla para la potencia.
Si r es cualquier número racional, excepto -1, entonces
Siguiendo a Leibniz, a veces usaremos el término integral indefinida en lugar de
antiderivada. Antiderivar también es integrar. En el símbolo 
se denomina signo de integral y f (x) se llama integrando.
3. Encuentre la antiderivada general de 
SOLUCIÓN:
Regla para la Sen y Cos
Las fórmulas de antiderivadas para las funciones seno y coseno se deducen directamente de la derivada
La integral indefinida es un operador lineal.
Suponga que f y g tienen antiderivadas (integrales indefinidas) y sea k una constante. Entonces:
4. Mediante la linealidad de 
evalúe:
SOLUCIÓN:
Aparecieron dos constantes arbitrarias C1 y C2, pero se combinaron en una constante, C
(b). Observe el uso de la variable u en lugar de x. Esto está bien mientras que el correspondiente símbolo de la diferencial sea du; entonces, tenemos un cambio completo en la notación.
Regla generalizada de la potencia
Sean g una función derivable y r un número racional diferente de -1. Entonces
5. Evalue:
SOLUCIÓN:
En este ejemplo(a), Leibniz usó la diferencial dx en su notación …dx Si hacemos u=g(x), entonces du = g'(x)dx.
Ejercicios
Encontrar la antiderivada general de los siguientes ejercicios y envia al correo siguiente: lsaucedoh@utrng.edu.mx
Aplicaciones de la derivada.
Ejemplo 1: Velocidad de un automóvil
Un automóvil se mueve en línea recta y su posición (en metros) en función del tiempo t(en segundos) está dada por:
s(t)=5t2+3t+2
Pregunta:
Encuentra la velocidad del automóvil en el instante t=4 segundos.
Solución:
La derivada de la posición representa la velocidad:
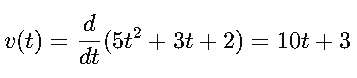
1. Estimación
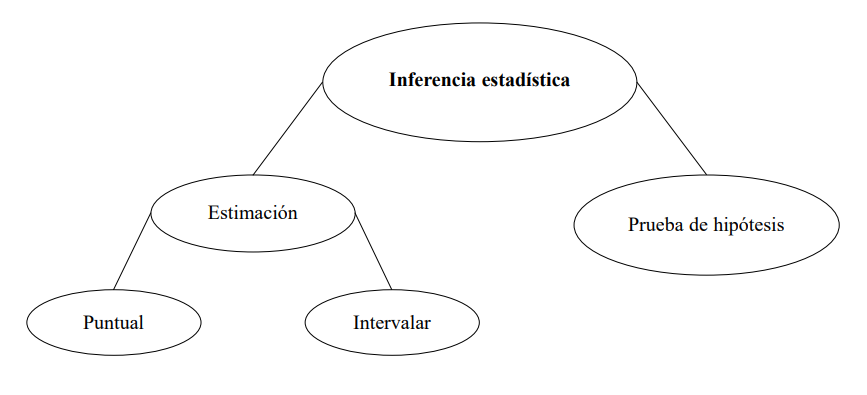
Existen dos métodos de inferencia en el enfoque clásico: la estimación y la prueba o contraste de hipótesis.
La estimación a su vez se da en dos formas: la puntual y la intervalar.
Por otro lado, la hipótesis se establece respecto al valor de las características de los parámetros y se evalúa con la información generada en una muestra. Si la evidencia no es consistente con la hipótesis propuesta, ésta se rechaza. Se llama “estadístico” a una función de los datos de la muestra.
2.1 Probabilidad básica y condicional
Técnicas de conteo
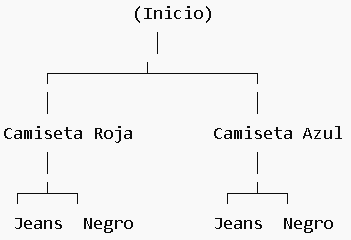
1. Diagrama de Árbol
Es una representación gráfica que muestra todas las posibles combinaciones de un evento paso a paso. Se usa cuando hay pocas opciones y queremos visualizar el problema.
Ejemplo:
Supongamos que tienes dos camisetas (roja y azul) y dos pantalones (jeans y negro). ¿Cuántas combinaciones diferentes de ropa puedes usar?
3. Introducción a la derivada
Concepto de derivada
Incremento
Si a la variable independiente x con un valor inicial a se le da un valor final b, a la diferencia b – a se le llama incremento de la variable x. Esto se expresa usando la letra griega delta (Δ) antes de la variable:
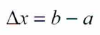
2. Continuidad
En un problema sobre continuidad podemos:
Primero. Determinar si una función f(.x) es continua o discontinua en un punto dado.
Segundo. Determinar en qué puntos una función/(.v) es discontinua.
Continuidad y Discontinuidad.
1. Sobre Conjuntos
Conjunto.
Es una colección de elementos considerada en sí misma como un objeto, que comparten entre sí características y propiedades semejantes.
a,b,c,d,… –> Letras que pueden considerarse elementos de un conjunto
A,B,C,D,.. –> Letras que podrían considerarse el nombre de un conjunto
4. Medidas de tendencia central, localización y dispersión
La Media o la Varianza son ejemplo de indicadores que se representan mediante las letras griegas μ, σ, ρ, etc., y se les llama parámetros. En el caso de una distribución de frecuencias también se pueden establecer medidas descriptivas y para distinguirlas de los parámetros, se usan letras latinas como x, s, r, etc.
1. Límites
Podríamos definir cálculo de esta manera:
El concepto de límite es primordial para muchos problemas en física, ingeniería y ciencias sociales. Básicamente, la pregunta es ésta: ¿qué le pasa con la función f(x) cuando x se acerca a alguna constante c? Existen variaciones de este tema, pero la idea básica es la misma en muchas circunstancias.
Podemos determinar áreas de rectángulos y triángulos por medio de fórmulas de geometría; pero, ¿qué hay de regiones con fronteras curvas, como un círculo? Arquímedes tuvo esta idea hace más de dos mil años. Imagine polígonos regulares inscritos en un círculo, como se muestra en la siguiente figura:
