Concepto de derivada

Incremento

Si a la variable independiente x con un valor inicial a se le da un valor final b, a la diferencia b – a se le llama incremento de la variable x. Esto se expresa usando la letra griega delta (Δ) antes de la variable:

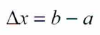
Ejemplos

---

Incremento de una función

Si y está en función de x, tenemos:

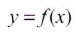
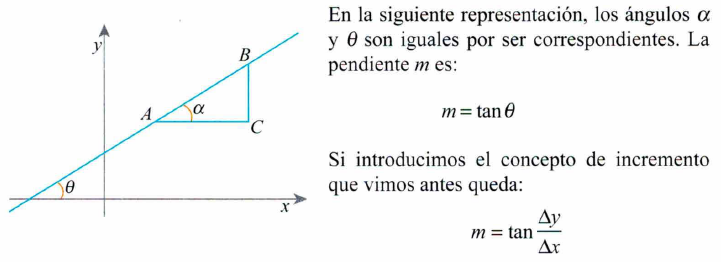
Sea el punto B(x,y) de una curva cuya ecuación es de la forma y =f(x):

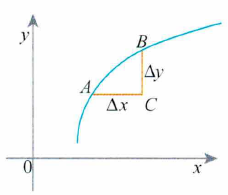
Los incrementos de x y de y son:

---

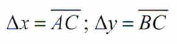
Pendiente de una línea recta

En geometría analítica estudiamos el tema de la pendiente m de una línea recta. A partir de esto, concluimos que:

• La pendiente de toda recta paralela al eje x es cero.
• La pendiente de una recta que forma un ángulo θ entre 0° < θ< 90° es positiva.
• Una recta paralela al eje y no tiene pendiente.
• Si la recta forma un ángulo θ entre 90° < θ < 180° la pendiente es negativa.

Debemos observar que cuando el punto B se mueve sobre la curva hacia A, la recta AB gira sobre A hasta coincidir con la recta AS; esta recta AS es tangente a la curva en A.

---

Derivada

Concepto de derivada

La derivada de una función con respecto a una variable es el límite, del incremento de la función entre el incremento de la variable, cuando el incremento de la variable tiende a cero.

Se expresa así:

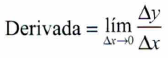
• Cuando el límite de la razón existe, se dice que la función tiene derivada.
• El valor de la derivada en cualquier punto de una curva es igual a la pendiente de la tangente a la curva en ese punto.

Notación de la derivada

La derivada se expresa en cualquiera de las formas siguientes:

Se sugiere acostumbramos a usar todas las notaciones para que se nos facilite la lectura de diferentes textos y porque cada una posee un uso cómodo, según el caso.

Regla general de la derivación

El proceso para obtener la derivada de una función f(x), incluye:

Ejemplos:

Aplica la regla general de la derivación y calcula la derivada de la siguiente función:

y=3x² + 4

Este resultado se puede expresar con cualquiera de las notaciones. También la forma siguiente se utiliza para indicar la operación que se requiere para obtener la derivada respecto a x.

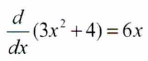
Esto se lee ‘”derivada de 3x² + 4 con respecto a x es igual a 6x” .

Ejemplo de una derivada: