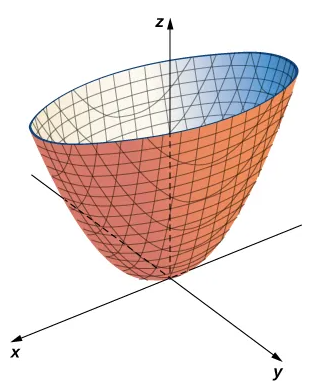
Superficies cuádricas
Hemos aprendido sobre las superficies en tres dimensiones descritas por ecuaciones de primer orden; estas son planos.
Otros tipos comunes de superficies pueden describirse mediante ecuaciones de segundo orden. Podemos ver estas superficies como extensiones tridimensionales de las secciones cónicas: la elipse, la parábola y la hipérbola. A estos gráficos los llamamos superficies cuádricas.
Definición
Las superficies cuádricas son los gráficos de las ecuaciones que pueden expresarse en la forma:
Ax2+By2+Cz2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0
Cuando una superficie cuádrica interseca un plano de coordenadas, la traza es una sección cónica.
Un elipsoide es una superficie descrita por una ecuación de la forma ![]() . Establezca x=0 para ver la traza del elipsoide en el plano yz. Para hallar las trazas en los planos xy y xz, establezca z=0 y y=0, respectivamente. Observe que, si a=b, la traza en el plano xy es un círculo. Del mismo modo, si a=c, la traza en el plano xz es un círculo y, si b=c, entonces la traza en el plano yz es un círculo. Una esfera, entonces, es un elipsoide con a=b=c.
. Establezca x=0 para ver la traza del elipsoide en el plano yz. Para hallar las trazas en los planos xy y xz, establezca z=0 y y=0, respectivamente. Observe que, si a=b, la traza en el plano xy es un círculo. Del mismo modo, si a=c, la traza en el plano xz es un círculo y, si b=c, entonces la traza en el plano yz es un círculo. Una esfera, entonces, es un elipsoide con a=b=c.
Ejemplo:
Dibujar el elipsoide:
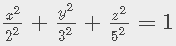
Solución: Empiece por dibujar las trazas. Para hallar la traza en el plano xy, establezca z=0: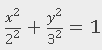 . Para hallar las otras trazas, primero establezca y=0 y luego establezca x=0.
. Para hallar las otras trazas, primero establezca y=0 y luego establezca x=0.
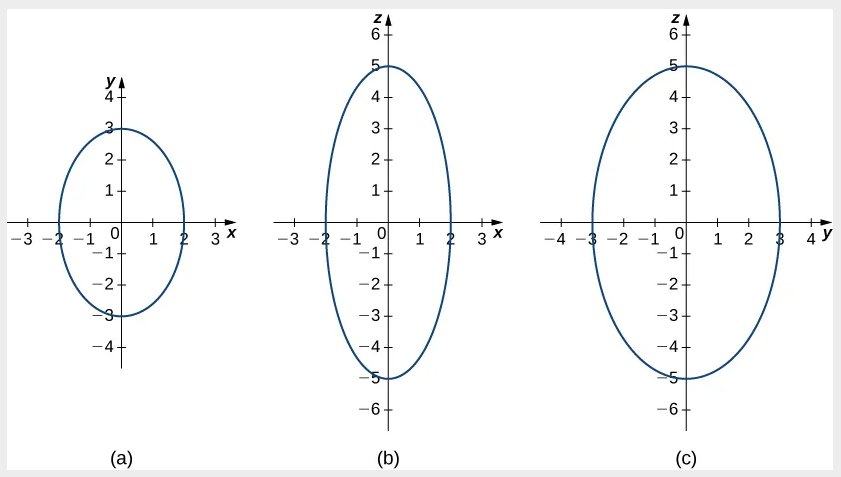
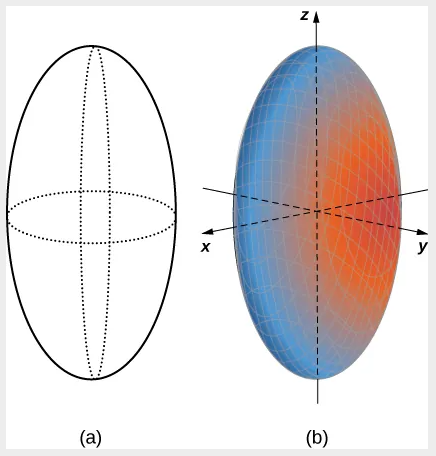
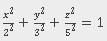 en el plano xy, cuando establecemos z=0. (b) Cuando establecemos y=0, obtenemos la traza del elipsoide en el plano xz, que es una elipse. (c) Cuando establecemos x=0, obtenemos la traza del elipsoide en el plano yz, que también es una elipse.
en el plano xy, cuando establecemos z=0. (b) Cuando establecemos y=0, obtenemos la traza del elipsoide en el plano xz, que es una elipse. (c) Cuando establecemos x=0, obtenemos la traza del elipsoide en el plano yz, que también es una elipse.Ahora que sabemos qué aspecto tienen las trazas de este sólido, podemos dibujar la superficie en tres dimensiones:
La traza de un elipsoide es una elipse en cada uno de los planos de coordenadas. Sin embargo, no es necesario que esto sea así para todas las superficies cuádricas. Muchas superficies cuádricas tienen trazas que son diferentes tipos de secciones cónicas, y esto se suele indicar con el nombre de la superficie. Por ejemplo, si una superficie se puede describir por una ecuación de la forma ![]() entonces llamamos a esa superficie un paraboloide elíptico. La traza en el plano xy es una elipse, pero las trazas en el plano xz y en el plano yz son parábolas. Otros paraboloides elípticos pueden tener otras orientaciones simplemente intercambiando las variables para darnos una variable diferente en el término lineal de la ecuación
entonces llamamos a esa superficie un paraboloide elíptico. La traza en el plano xy es una elipse, pero las trazas en el plano xz y en el plano yz son parábolas. Otros paraboloides elípticos pueden tener otras orientaciones simplemente intercambiando las variables para darnos una variable diferente en el término lineal de la ecuación ![]() o
o ![]()