Ejemplo 1: Velocidad de un automóvil
Un automóvil se mueve en línea recta y su posición (en metros) en función del tiempo t(en segundos) está dada por:
s(t)=5t2+3t+2
Pregunta:
Encuentra la velocidad del automóvil en el instante t=4 segundos.
Solución:
La derivada de la posición representa la velocidad:
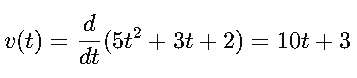
Evaluamos en t=4:
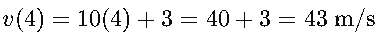
La velocidad en t=4 segundos es 43 m/s, lo que significa que el automóvil se está moviendo a esa rapidez en ese instante.
Ejemplo 2: Crecimiento de una población
El tamaño de una población de bacterias en un laboratorio está modelado por la función:
P(t)=500e0.2t
donde P(t) es el número de bacterias y t el tiempo en horas.
Pregunta:
Encuentra la tasa de crecimiento de la población en t=5 horas.
Solución:
La derivada de la población representa la tasa de crecimiento:
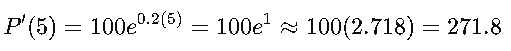
A las 5 horas, la población de bacterias está creciendo a una tasa de 271.8 bacterias por hora. Esto significa que en ese momento, la cantidad de bacterias está aumentando rápidamente.
Ejemplo 3: Máxima ganancia en una empresa 💰
Una empresa vende un producto y su función de ingresos (en miles de dólares) en función del precio x (en dólares) es:
R(x)=−2x2+40x
Pregunta:
Encuentra el precio que maximiza los ingresos.
Solución:
La derivada de los ingresos representa la tasa de cambio de los ingresos con respecto al precio. Buscamos el máximo resolviendo R′(x)=0:
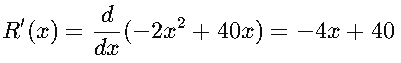
Igualamos a 0:
−4x+40=0
x=10
El precio que maximiza los ingresos es 10 dólares. Vender el producto a este precio generará la mayor cantidad de ingresos para la empresa.
Ejercicios:
Ejemplo 1: Caída de un objeto 🏀
Un objeto es lanzado hacia arriba desde una altura de 80 metros con una velocidad inicial. Su altura en función del tiempo ttt (en segundos) está dada por:
h(t)=80+20t−5t2
Pregunta:
¿Cuál es la velocidad del objeto en el instante t=3 segundos?
Ejemplo 2: Crecimiento de un árbol
La altura de un árbol (en metros) después de ttt años está dada por la función:
H(t)=3t2+2t+1
Pregunta:
¿Cuál es la tasa de crecimiento del árbol a los 5 años?
Ejemplo 3: Maximización de producción en una fábrica
Una fábrica produce un artículo y su productividad (en unidades producidas por hora) depende del número de trabajadores xxx según la función:
P(x)=−x2+10x
Pregunta:
¿Cuántos trabajadores deben contratarse para maximizar la producción?
INSTRUCCIONES:
Resolver y enviar desarrollo e interpretacion de los resultados al correo lsaucedoh@utrng.edu.mx , agregando sus datos(nombre y grupo)