El objetivo principal del cálculo integral es obtener el límite de la suma de un gran número de magnitudes, cada una de las cuales tiende a cero

El filósofo Brison, contemporáneo de Sócrates, trató de calcular el área de un círculo por medio de polígonos regulares inscritos y circunscritos al círculo. Este legendario método se conoce como proceso de reducción porque a medida que el número de lados de un polígono aumenta, la diferencia entre las áreas de éstos se va reduciendo.

La importancia de esta técnica la podemos observar si se plantea el problema siguiente:

• Calcular el área A de la superficie limitada por la parábola y = x² + 1 y las rectas y = 1, x = 0, x = 4

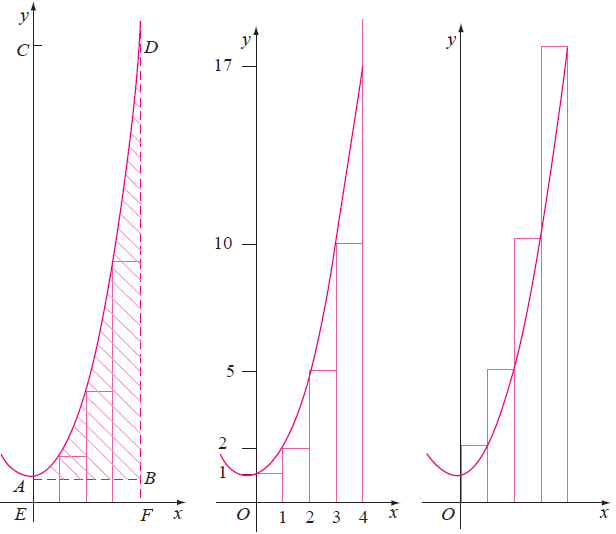
La suma de las áreas de las dos series de rectángulos se presenta a continuación. En la figura 2 todos los rectángulos tienen base 1:

En la figura 3 todos los rectángulos tienen base 1:

El área para obtener está en 18 y 34 unidades cuadradas: 18 < A < 34

Suma de Riemann

La sumatoria de n términos {a₁, a₂, a₃,…a_n} se expresa así:

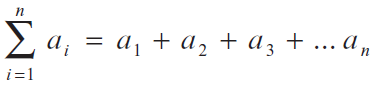
De donde:

**Algunos autores usan la palabra límite en lugar de extremos.

---

Ejemplo 1:

Calcula la siguiente sumatoria:

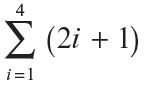
En este ejemplo, a_i = (2_i + 1). Para calcular la suma sustituimos la i sucesivamente por los enteros 1, 2, 3, 4 desde el 1 hasta el 4, que en el ejemplo son los externos de la sumatoria, luego se suman los términos así obtenidos:

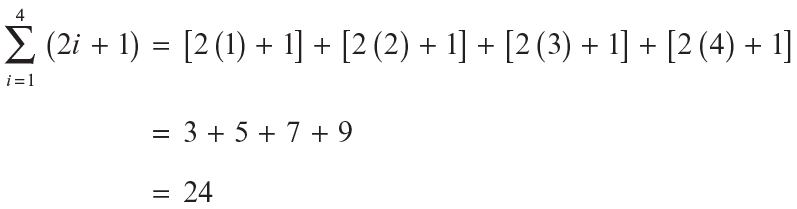
Cualquier variable se puede usar como índice de la sumatoria. Sin embargo, es muy común preferir las letras i, j, k porque normalmente están asociadas con los enteros. El extremo inferior no tiene que ser necesariamente el número 1, pues cualquier número entero menor o igual al extremo superior es válido.

---

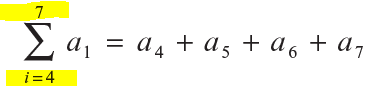
Ejemplo 2:

Calcula las siguientes suma:

---

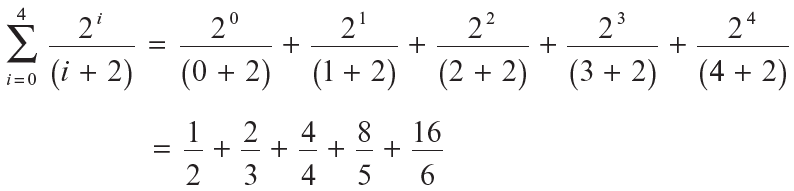
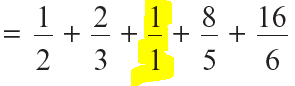
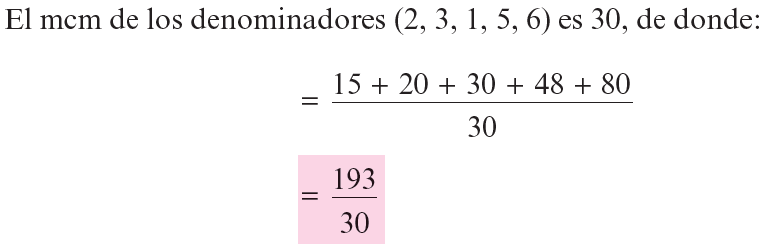
Propiedades de las sumas de Riemann

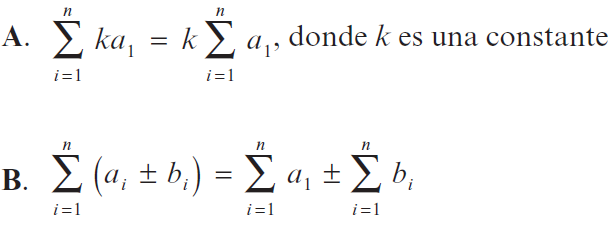
Ejemplo de las propiedades:

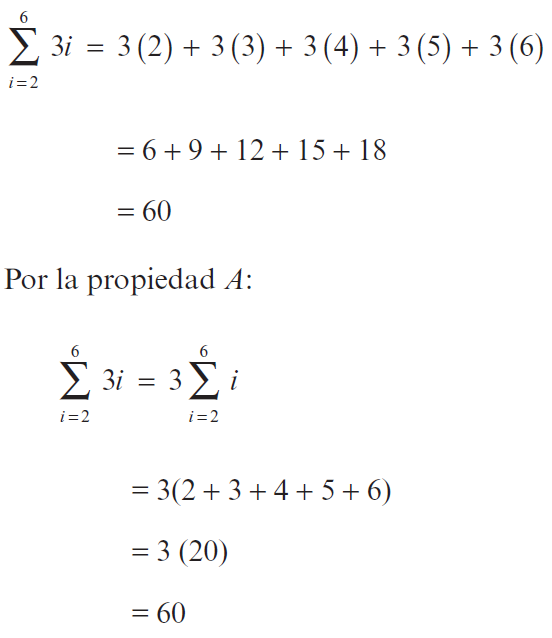
Fórmulas de las sumas de Riemann

---

Ejercicios:

---

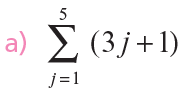
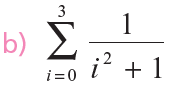
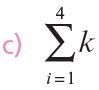
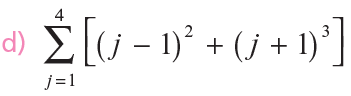
Propiedades de la integral definida

A.

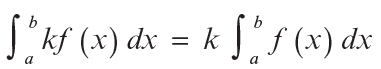
B.

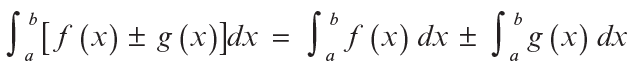
Ejemplos de las propiedades A y B

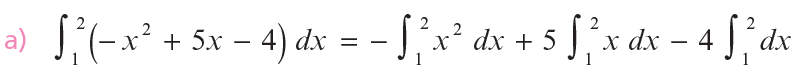
Integramos por separado cada integral:

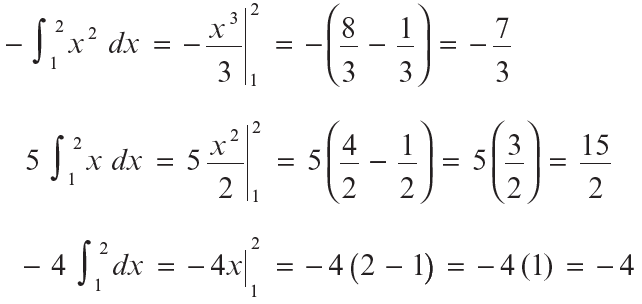
Por lo tanto,

---

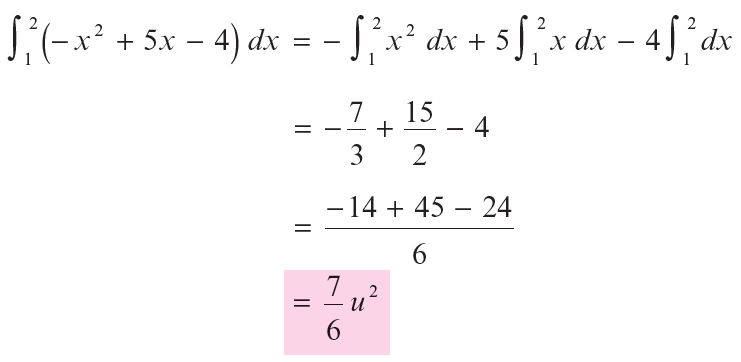
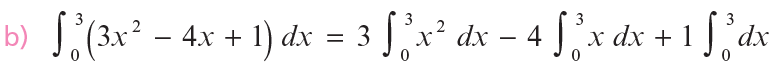
Integramos por separado cada integral:

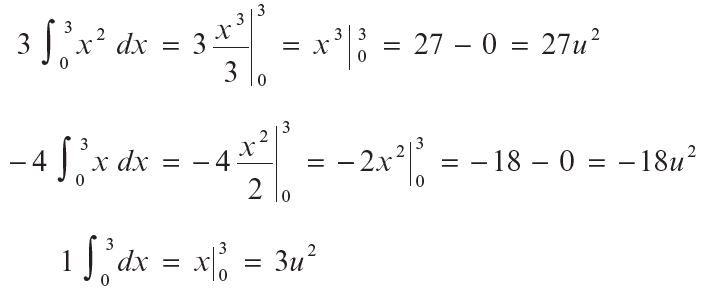
Por lo tanto,

---

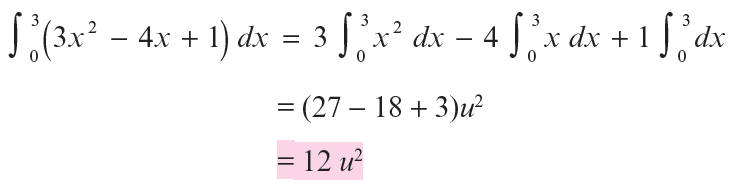
Ejercicios:

A.

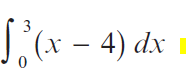
B.

---

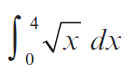
Teorema fundamental del cálculo

El teorema fundamental del cálculo establece que si una función f es continua en el intervalo [a, b], entonces:

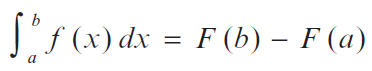
donde F es cualquier función tal que F=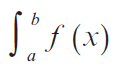para toda x en [a, b].

Áreas

Por el teorema fundamental de cálculo sabemos que si f es una función continua en el intervalo [a, b], entonces existe la integral definida 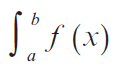dx. El resultado de esta integral es igual al área bajo la curva f (x) representada en el plano.