El objetivo principal del cálculo integral es obtener el límite de la suma de un gran número de magnitudes, cada una de las cuales tiende a cero

El filósofo Brison, contemporáneo de Sócrates, trató de calcular el área de un círculo por medio de polígonos regulares inscritos y circunscritos al círculo. Este legendario método se conoce como proceso de reducción porque a medida que el número de lados de un polígono aumenta, la diferencia entre las áreas de éstos se va reduciendo.

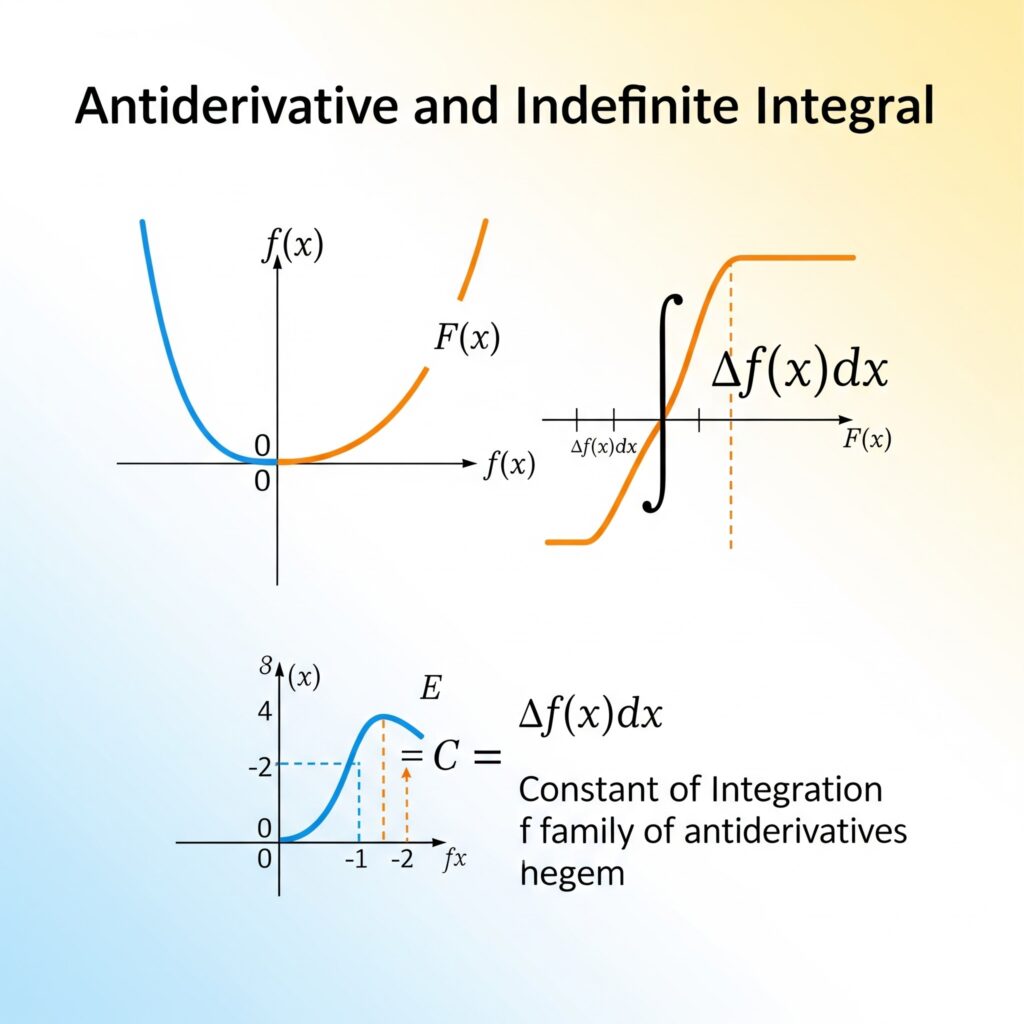
Antiderivadas

La mayoría de las operaciones matemáticas con que trabajamos vienen en pares de inversas: suma y resta, multiplicación y división, y exponenciación y extracción de raíces. Una razón de operaciones inversas es su utilidad en la resolución de ecuaciones. Por ejemplo, la resolución de x³ = 8, esto implica el uso de extraer raíces.