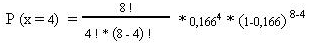Técnicas de conteo
1. Diagrama de Árbol
Es una representación gráfica que muestra todas las posibles combinaciones de un evento paso a paso. Se usa cuando hay pocas opciones y queremos visualizar el problema.
Ejemplo:
Supongamos que tienes dos camisetas (roja y azul) y dos pantalones (jeans y negro). ¿Cuántas combinaciones diferentes de ropa puedes usar?
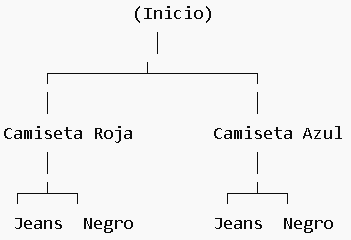
Hay 4 combinaciones posibles:
- Roja – Jeans
- Roja – Negro
- Azul – Jeans
- Azul – Negro
2. Regla Multiplicativa
Si un evento ocurre en m formas y otro evento ocurre en n formas, entonces el número total de maneras en que ambos pueden ocurrir es m × n.
Ejemplo:
Si un restaurante ofrece 3 entradas y 4 platos principales, el número total de comidas posibles es:
3×4=12
Así que hay 12 combinaciones diferentes de comida.
3. Combinación
Se usa cuando el orden NO importa. Se calcula con la fórmula:
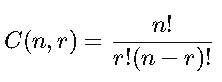
Donde:
- n es el número total de elementos.
- r es el número de elementos seleccionados.
- ! significa «factorial», es decir, el producto de los números enteros positivos hasta ese número.
Ejemplo:
En una rifa hay 5 boletos numerados del 1 al 5, y se van a elegir 2 ganadores sin importar el orden.
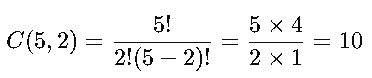
Hay 10 formas diferentes de elegir los 2 ganadores.
4. Permutación
Se usa cuando el orden SÍ importa. Se calcula con la fórmula:
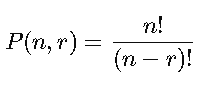
Ejemplo:
Si en una carrera de 8 corredores, queremos saber de cuántas formas se pueden asignar los primeros 3 lugares, calculamos:
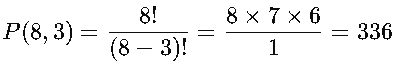
Hay 336 maneras de asignar los 3 primeros lugares.
Comparación de técnicas.

Distribuciones Discretas de Probabilidad
Concepto de Variable Aleatoria Discreta
Una variable aleatoria discreta es aquella que solo puede tomar valores específicos y contables (como números enteros). Se usa para modelar situaciones donde los resultados ocurren en conteos finitos o infinitos numerables.
🔹 Ejemplo:
El número de veces que una moneda cae en cara al lanzarla 5 veces. Puede tomar valores: 0, 1, 2, 3, 4 o 5.
Distribuciones de Probabilidad Discretas
A) Distribución Binomial
Se usa cuando hay una cantidad fija de ensayos n, donde cada uno tiene solo dos posibles resultados: éxito (p) o fracaso (1−p).
🔹 Fórmula:
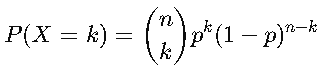
Donde:
- n = número de ensayos.
- k = número de éxitos deseados.
- p = probabilidad de éxito en cada ensayo.
🔹 Ejemplo:
Si lanzamos una moneda 4 veces y queremos saber la probabilidad de obtener exactamente 2 caras:
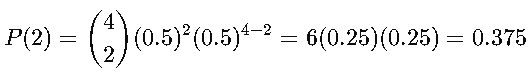
Así que hay 37.5% de probabilidad de obtener exactamente 2 caras.
Distribución Hipergeométrica
Se usa cuando se seleccionan elementos sin reemplazo de un grupo finito, lo que significa que la probabilidad de éxito cambia en cada selección.
🔹 Fórmula:
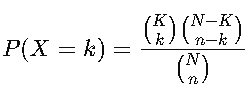
Donde:
- N = tamaño total de la población.
- K = número total de éxitos en la población.
- n = número de elementos seleccionados.
- k = éxitos deseados en la muestra.
🔹 Ejemplo:
En una caja hay 10 bolas: 4 rojas y 6 azules. Se extraen 3 bolas al azar sin reemplazo. ¿Cuál es la probabilidad de obtener exactamente 2 bolas rojas?
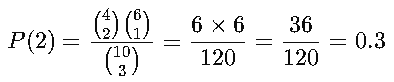
Hay 30% de probabilidad de extraer exactamente 2 bolas rojas.
Distribución de Poisson
Se usa para contar el número de eventos que ocurren en un intervalo de tiempo o espacio, donde los eventos son raros y ocurren con una tasa media λ.
🔹 Fórmula:
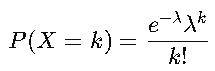
Donde:
- λ = número promedio de eventos en el intervalo.
- k = número de eventos que queremos calcular.( es lo que se pregunta)
- e ≈ 2.718 (constante matemática).
🔹 Ejemplo:
Si en una tienda llegan en promedio 5 clientes por hora, ¿cuál es la probabilidad de que lleguen exactamente 3 clientes en una hora?
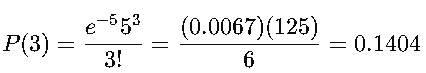
Hay 14.04% de probabilidad de que lleguen exactamente 3 clientes en una hora.
Comparación de las Distribuciones

Ejercicios
Ejercicio 1
-sobre binomial-
¿Cuál es la probabilidad de obtener cuatro veces el número 3 al lanzar un dado ocho veces?=0.026->demostrarlo
k=4(número de aciertos)
n=8
p=1/6=0.166(probabilidad de que salga un 3 al tirar el dado)
La fórmula queda:
Ejercicio 2
-sobre poisson-
La probabilidad de que un niño nazca pelirrojo es de 0,012. ¿Cuál es la probabilidad de que entre 800 recien nacidos haya 5 pelirrojos= 4,602->demostrarlo