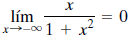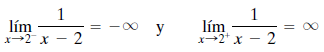En un problema sobre continuidad podemos:
Primero. Determinar si una función f(.x) es continua o discontinua en un punto dado.
Segundo. Determinar en qué puntos una función/(.v) es discontinua.
Continuidad y Discontinuidad.

Ejemplos:




En algunos casos la discontinuidad es evitable asignando a la función otro valor para f(a ).
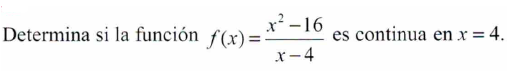

En este caso, la discontinuidad es evitable porque si asignamos a la función
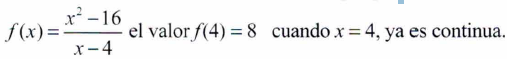
Límites al infinito;
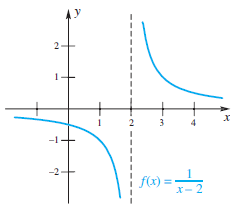
límites infinitos

Cuando escribimos x ⇾ ∞, no queremos dar a entender que en un lugar muy alejado a la derecha del eje x exista un número —más grande que todos los demás— al cual se aproxima x. En lugar de eso utilizamos x ⇾ ∞ como una forma breve de decir que x se hace cada vez más grande sin cota.
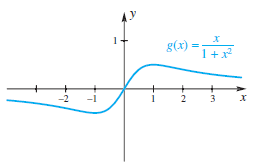
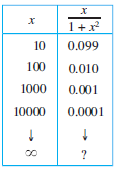
En la siguiente tabla de la figura, hemos listado valores de g(x) = x / (1 + x2) para diversos valores de x. Parece que g(x) se hace cada vez más pequeño conforme x se hace cada vez más grande. Escribimos
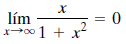
Al experimentar con números negativos cada vez más lejanos del cero nos conduciría a escribir