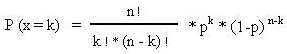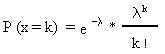La distribución de probabilidad de este tipo de distribución sigue el siguiente modelo:

Ejemplo:

 ¿Cuál es la probabilidad de obtener 6 caras al lanzar una moneda 10 veces?

” k “ es el número de aciertos. En cada acierto decíamos que la variable toma el valor 1: como son 6 aciertos, entonces k = 6

” n” es el número de ensayos. En nuestro ejemplo son 10

” p “ es la probabilidad de éxito, es decir, que salga “cara” al lanzar la moneda. Por lo tanto p = 0,5

La fórmula quedaría:

por lo tanto:

P( x = 6 ) = 0.205

Las distribución de Poisson parte de la distribución binomial:

Cuando en una distribución binomial se realiza el experimento un número “n” muy elevado de veces y la probabilidad de éxito “p” en cada ensayo es reducida, entonces se aplica el modelo de distribución de Poisson:

Se tiene que cumplir que:

” p ” < 0.10

” p * n “ < 10

La distribución de Poisson sigue el siguiente modelo:

El número “e” es 2,71828.

” l “ = n * p (es decir, el número de veces n que se realiza el experimento multiplicado por la probabilidad p de éxito en cada ensayo)

” k ” es el número de éxito cuya probabilidad se está calculando.

Ejemplo:

La probabilidad de tener un accidente de tráfico es de 0,02 cada vez que se viaja, si se realizan 300 viajes, ¿cual es la probabilidad de tener 3 accidentes?

Como la probabilidad ” p ” es menor que 0,1, y el producto ” n * p ” es menor que 10, entonces aplicamos el modelo de distribución de Poisson.

quedando:

P ( x = 3 ) = 0.0892

Por lo tanto, la probabilidad de tener 3 accidentes de tráfico en 300 viajes es del 8,9%

Ejercicio 1

-sobre binomial-

¿Cuál es la probabilidad de obtener cuatro veces el número 3 al lanzar un dado ocho veces?=0.026->demostrarlo

k=4(número de aciertos)

n=8

p=1/6=0.166(probabilidad de que salga un 3 al tirar el dado)

La fórmula queda:

Ejercicio 2

-sobre poisson-

La probabilidad de que un niño nazca pelirrojo es de 0,012. ¿Cuál es la probabilidad de que entre 800 recien nacidos haya 5 pelirrojos= 4,602