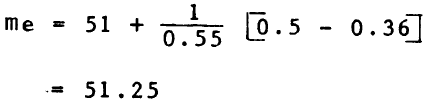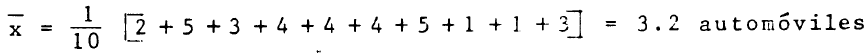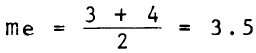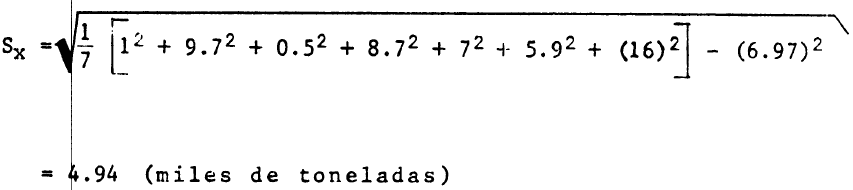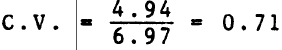Ejemplo 1
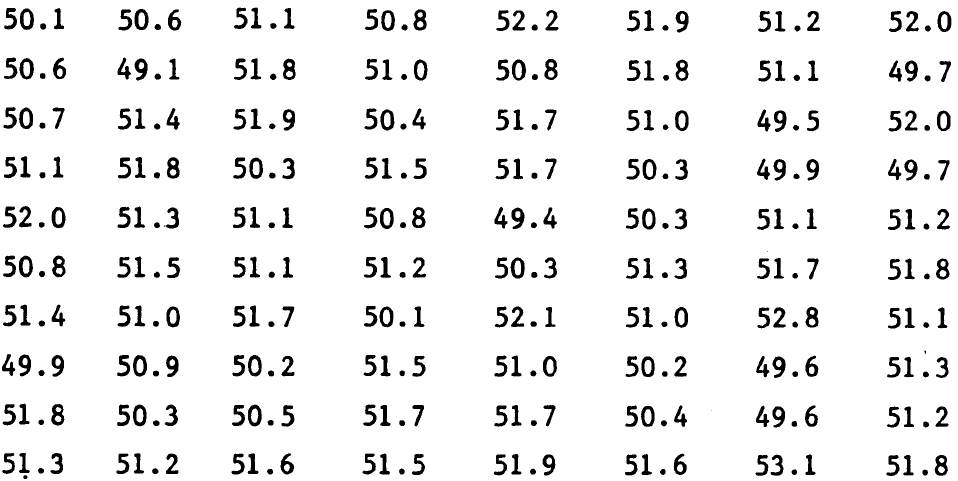
Los siguientes datos representan la longitud en centímetros de 80 piezas de madera que fueron seleccionadas en una bodega. Se desea presentar los datos en forma resumida y ordenada.
Como primer paso, se debe calcular el rango de la muestra que se define como la diferencia entre el mayor y el menor de los elementos. Así, para los datos anteriores:
rango = 53.1 – 49.1 = 4.0
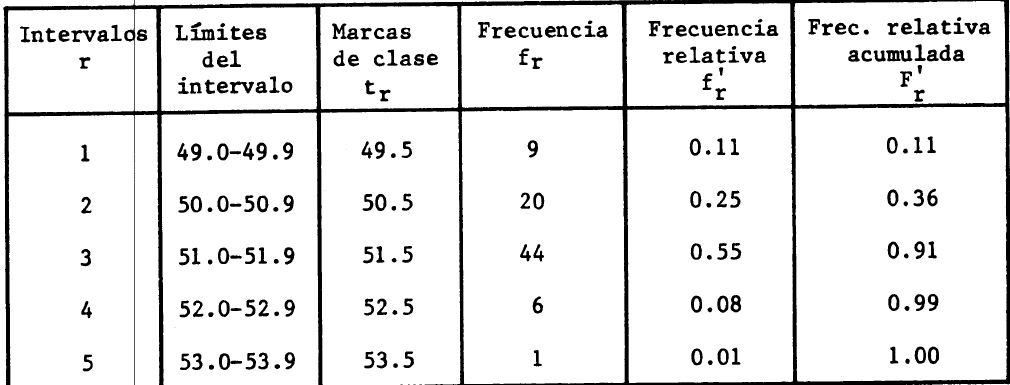
En las dos dos primeras columnas de la siguiente tabla se muestran los intervalos y marcas de clase (tr) de la muestra que se esta ordenando.
La media:
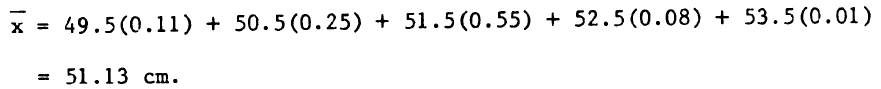
La mediana

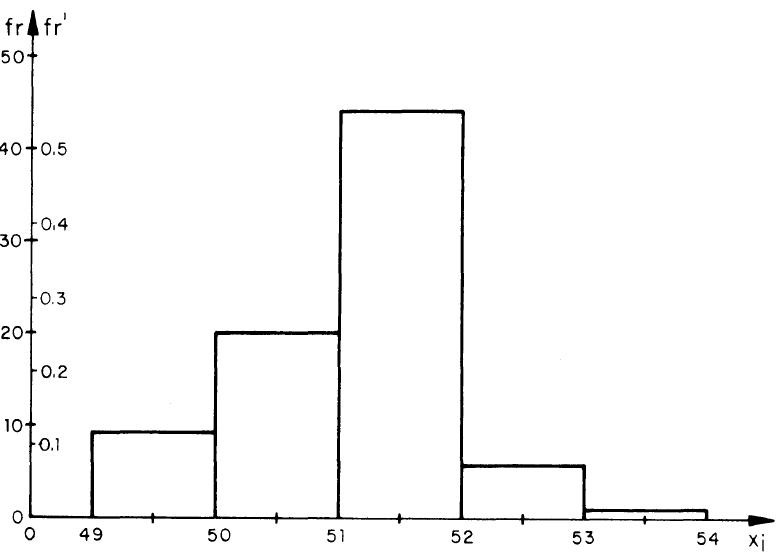
Para representar las frecuencias o las frecuencias relativas se usa generalmente el histograma o polígono de Frecuencias. En el histograma, la frecuencia se considera constante en todos los puntos de cada intervalo de clase, por lo que se representa como una sucesión de rectángulos del mismo ancho y cuyas alturas corresponden a las frecuencias o a las frecuencias relativas acumuladas de los intervalos correspondientes.
Ejemplo 2
El número de automóviles que se vende semanalmente en una agencia distribuidora, se ha registrado durante diez semanas con los siguientes resultados:
2,5,3,4,4,4,5,1,1,3
¿Cuál es la media muestral?
Cuál es la mediana de la muestra?. ordenando los elementos en forma ascendente, se obtiene:
1,1,2,3,3,4,4,4,5,5
como son diez elementos, la mediana se encuentra entre el quinto(3) y el sexto elemento (4), por lo cual:
Ejemplo 3
La producción de mineral de fierro en siete países, latinoamericanos, durante el año 2016, fue la siguiente:
1,9.7,0.5,8.7,7,5,9,16(miles de toneladas).
Obtener:
- La media.
- La desviación estándar.
- El coeficiente de variación.
La media:
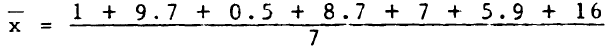
= 6.97 (miles de toneladas)
La desviación estándar:
Coeficiente de variación: