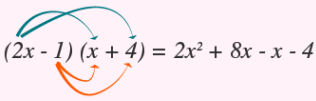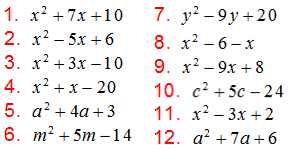Cuando nos encontramos con un trinomio cuadrado perfecto
X2 + 8x + 16 = 0
X2 + 8x + 16 = 0 Nos damos cuenta de que es un Trinomio cuadrado perfecto. Sabemos que es perfecto cuando la raíz cuadrada del término cuadrático(1) y el término Lineal(16) son números enteros.
- (x + _____ )(x + _____) = 0 Colocamos los paréntesis y buscamos los valores que satisfagan la ecuación, es decir que multiplicados den 16 y sumados den 8.
- (x + 4)(x + 4) = 0 Factorizando como un binomio al cuadrado aquí mostrado en forma de factores
- x+4=0 | x+4=0 Aplicando la propiedad del producto nulo.
- x1=−4 | x2=−4 Despejando.
Cuando nos encontramos con un trinomio cuadrado No perfecto
2x2 + 7x − 4 = 0
2x2 + 7x − 4 = 0 No es un trinomio cuadrado perfecto, porque la raíz cuadrada del término cuadrático (2) y el término lineal (7) deben ser números enteros y en este caso no lo son, entonces hay que buscar dos números que multiplicados den 2 y otros dos que multiplicados den 4
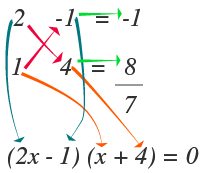
Una vez encontrados los valores que satisfacen el punto anterior, los colocamos de la siguiente manera, para que al multiplicar de forma cruzada y sumar estos valores nos dé como resultado el coeficiente del término lineal. En este caso para que la suma dé 7 debemos agregar un signo menos, pero los signos se agregan en la segunda columna.Solo falta ordenar los términos encontrados en los paréntesis.
Antes de proceder a encontrar las soluciones hay que verificar si el producto de los binomios cumple con la ecuación original. Para ello se multiplica como lo indican las flechas.
Ordenando términos:
(2x − 1) (x + 4)= 2x2 + 7x – 4
Aplicando la propiedad del producto nulo:
2x − 1 = 0 x + 4 = 0
Despejando:
x1=½ x2=−4
Ejercicios