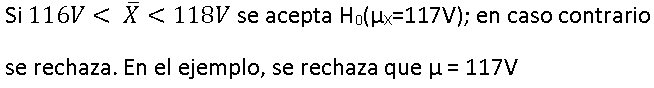H0, Hn, Errores Tipo I y II
La prueba de hipótesis estadística es otra forma de inferencia que se utiliza para aceptar o rechazar hipótesis sobre un fenómeno aleatorio;no se puede considerar como una prueba definitiva, ya que en ella se establece un criterio o regla de decisión para aceptar o rechazar una hipótesis y, la regla de decisión está asociada con ciertos riesgos.
Procedimiento General
En primer lugar, para realizar una prueba de hipótesis estadística se debe plantear el enunciado en cuestión, en términos de parámetros poblacionales como la media, la varianza, etcétera.
Declarar los tipos de Hipótesis que observemos, Hipótesis Nula(H0) y las Hipótesis alternas(H1, H2, …).
La Hipótesis Nula es la que se toma como referencia en la prueba, se plantea como una igualdad de la forma Θ=Θ0, donde Θ0 es un valor supuesto del parámetro Θ.
Las Hipótesis Alternas son aquellas que difieren de H0 y pueden tener la forma:
- Θ ≠ Θ0
- Θ > Θ0
- Θ < Θ0
Es importante señalar, que aceptar como verdadera una hipótesis alterna equivale a rechazar la hipótesis nula correspondiente
y cuando se acepta H0 , se rechaza como verdadera
H1 (considerando que es la única alternativa). Lo más importante de una prueba estadística es el diseño de una Regla de decisión, la cual señala en qué casos se debe acepta o rechazar la hipótesis nula en función de lo que indica un estadístico, obtenido de una muestra representativa.
Ejemplo
Si un técnico de la CFE asegura que, en promedio, el voltaje que reciben los usuarios en cierta zona de la ciudad es de 117 volts
El voltaje promedio(μX), el enunciado está expresado en términos de la media poblacional, por lo que la Hipótesis Nula es:
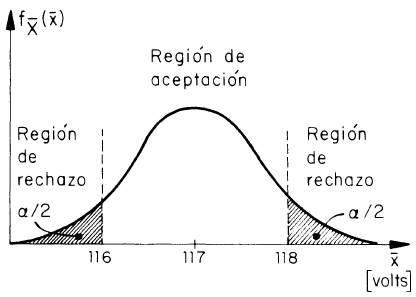
H0 : μX = 117V
La Hipótesis Alterna debe plantearse de acuerdo con los resultados que se desean obtener de la prueba, en este caso, hay que tratar de encontrar evidencias que muestren que el voltaje es diferente de 117V, sin importar si es mayor o menor.
H1 : μX ≠ 117V
Cuando el interés está centrado en uno de los extremos de la variable aleatoria, como en la vida útil de una máquina o las utilidades de una empresa, en donde solamente importa un aumento, entonces la hipótesis alterna sería de la forma:
H1 : Θ > Θ0
Por lo anterior cuando la Hipótesis Alterna es de la forma Θ > Θ0 ó Θ < Θ0 se le denomina como Unilateral o de Una Cola y si es de la forma Θ ≠ Θ0 , se le llama Bilateral o de Dos Colas.
Para establecer la Regla de Decisión se toma como base una distribución muestral; en el ejemplo 1 a distribución muestral de la media (
) sería la más adecuada. Posteriormente se fija una región de aceptación y una de rechazo en el dominio del estadístico, es decir que si para una muestra,
el estadístico toma un valor en la región de aceptación, entonces se considera que la hipótesis nula es verdadera; en caso contrario, se piensa que es falsa.
Errores en las decisiones estadísticas
Como 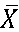es una variable aleatoria, al seguir la Regla de Decisión se corre el riesgo de Rechazar la Hipótesis Nula, cuando 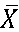tome un valor en la región de rechazo y corresponda a una población con media μX = 117V, esto significa que se está rechazando una Hipótesis nula que es Verdadera.
A este Error, se le conoce como de Tipo I y la probabilidad de cometerlo se le llama Nivel de Significación y se representa con ∝
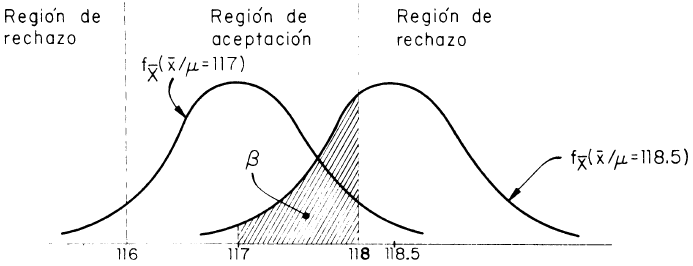
Otro error que puede cometerse al decidir sobre la veracidad de una hipótesis nula, basándose en la regla de decisión, es el denominado Error Tipo II, que consiste en aceptar una Hipótesis nula que es Falsa. Debido a que no se llega a conocer el verdadero valor del parámetro poblacional, se pueden suponer algunos de esos y calcular la probabilidad o riesgo de cometer el error de tipo II, esta probabilidad se representa mediante β.
En el ejemplo del voltaje, si la media poblacional fuera de 118.5V en lugar de 117V, el área bajo la gráfica de la distribución muestral cuya media es μ = 118.5V y que se encuentra en la región de aceptación, es la probabilidad de cometer el error de tipo II( β ).
Para establecer una regla de decisión, lo más deseable es que la probabilidad de cometer los errores de tipo I y II sea mínima.
La única manera efectiva de reducir los valores de ∝ y β es aumentando el tamaño de la muestra, pues de esa manera se reduce la dispersión de la distribución muestral.
En resumen, para efectuar una prueba de hipótesis se debe seguir el siguiente procedimiento:
- Establecer las hipótesis nula y alterna.
- Seleccionar el nivel de significación que será utilizado.
- Calcular los puntos críticos del estadístico de prueba.
- Establecer la regla de decisión.
- Determinar, de acuerdo con la regla, si se acepta o se
rechaza. la hipótesis nula.
Este procedimiento puede aplicarse en cualquier prueba de hipótesis y a pesar de que se ilustró en un caso bilateral, es muy semejante la aplicación en una prueba estadística unilateral.