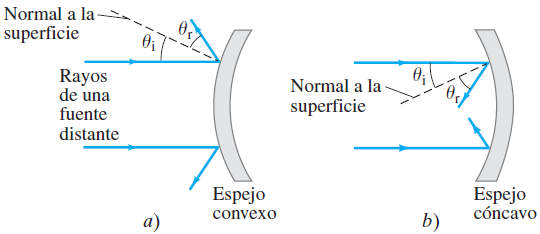
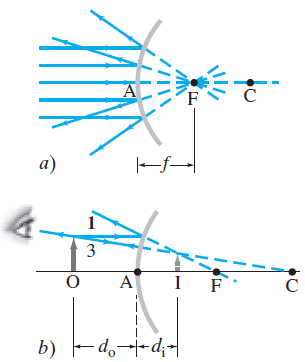
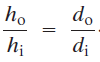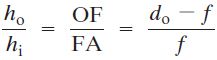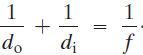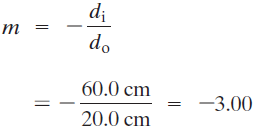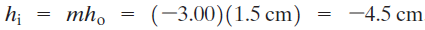Las superficies reflectantes no tienen que ser planas. Los espejos curvos más comunes son esféricos, lo que significa que forman una sección de una esfera. Un espejo esférico se llama convexo si la reflexión tiene lugar en la superficie exterior de la forma esférica, de manera que el centro de la superficie del espejo sobresale hacia el observador(figura a). Un espejo se llama cóncavo si la superficie reflectante está en la superficie interior de la esfera, de manera que el centro del espejo se aleja del observador
(como una “cueva”), figura b. Los espejos cóncavos se usan como espejos de afeitado o con fines cosméticos porque amplifican, y los espejos convexos a veces se usan en los autos y camiones (espejos retrovisores) y en las tiendas, pues tienen un amplio campo de visión.

• 

• 

Punto Focal y Distancia Focal.

Para ver cómo forman imágenes los espejos esféricos, considere primero un objeto que está muy lejos de un espejo cóncavo. En el caso de un objeto distante, como se ilustra en la siguiente figura, los rayos provenientes de cada punto del objeto, que inciden sobre el espejo, serán casi paralelos.

En el caso de un objeto infinitamente distante (el Sol y las estrellas se aproximan a esto), los rayos serían precisamente paralelos. Considere ahora tales rayos paralelos que inciden sobre un espejo cóncavo, como en la siguiente figura.

La ley de reflexión se sostiene para cada uno de estos rayos en el punto donde cada uno incide sobre el espejo. Como se observa, no todos llegan a un solo punto. Para formar una imagen clara, los rayos deben llegar a un punto. En consecuencia, un espejo esférico no formará una imagen tan clara como la de un espejo plano. Sin embargo, como se muestra a continuación, si el espejo es pequeño comparado con su radio de curvatura, de manera que un rayo reflejado forme sólo un ángulo pequeño con el rayo incidente (2θ en la figura), entonces los rayos se cruzarán unos a otros muy aproximadamente en un solo punto, o foco.

En el caso que se ilustra en la figura anterior, los rayos incidentes son paralelos al eje principal, que se define como la línea recta perpendicular a la superficie curva en su centro (línea CA en la figura). El punto F, donde los rayos paralelos incidentes llegan a un foco después de la reflexión, se llama punto focal del espejo. La distancia entre F y el centro del espejo, longitud FA, se llama distancia focal o longitud focal, f, del espejo. El punto focal también es el punto de la imagen para un objeto infinitamente alejado a lo largo del eje principal. La imagen del Sol, por ejemplo, estaría en F.

Para un espejo cuya superficie reflectante es pequeña en comparación
con su radio de curvatura, que los rayos casi se encuentran en un punto común, F, y también se calculará la distancia focal f. En esta aproximación, sólo se consideran los rayos que forman un ángulo pequeño con el eje principal; tales rayos se llaman rayos
paraxiales. En esta aproximación, FA = FC. Pero FA = f, la distancia focal, y CA =2 x FA = r. En consecuencia, la distancia focal es la mitad del radio de curvatura:

Formación de imágenes; diagramas de rayos.

Entonces, para un objeto en el infinito, la imagen se ubica en el punto focal de un espejo esférico cóncavo, donde f = r/2. Pero, ¿dónde se encuentra la imagen para un objeto que no está en el infinito?

Primero considere el objeto que se representa como una flecha en la figura a), que está entre F y C en el punto O (O por objeto). Ahora se determinará dónde estará la imagen para un punto dado O’ en la parte superior del objeto.

Para hacer esto, se pueden dibujar varios rayos y asegurarse de que se reflejan en el espejo de tal modo que el ángulo de reflexión sea igual al ángulo de incidencia. Se podrían dibujar muchos rayos que salen de cualquier punto del objeto, pero la determinación de la posición de la imagen se simplifica si se trata con tres rayos particularmente simples.
Éstos son los rayos marcados como 1, 2 y 3 en las figuras a), b) y c), y se les dibuja saliendo del punto O’ del objeto del modo siguiente:

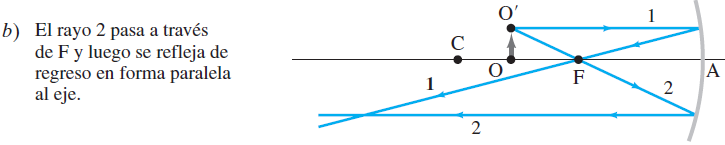
El rayo 1 se dibuja paralelo al eje; por lo tanto, después de la reflexión, debe pasar a lo largo de una línea a través de F (a).
El rayo 2 sale de O’ y pasa a través de F (b); por lo tanto, se debe reflejar
de manera que sea paralelo al eje.
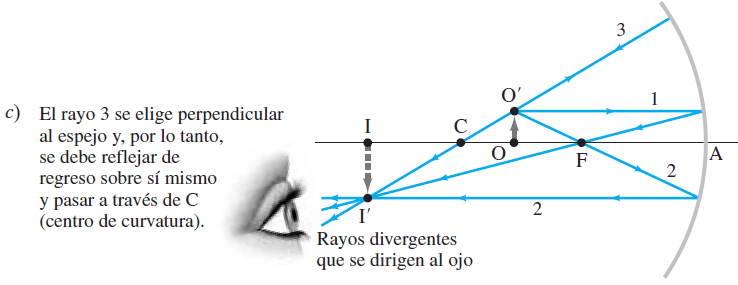
El rayo 3 pasa a través de C, el centro de curvatura (c); está a lo largo
de un radio de la superficie esférica y es perpendicular al espejo, así que se refleja de regreso sobre sí mismo.

La imagen en las figuras a, b, y c es visible al ojo cuando éste se coloca a la izquierda de la imagen, de manera que parte de los rayos que divergen desde cada punto de la imagen(como el punto I’) pueden entrar al ojo como se muestra en la figura(c).

Ecuación del Espejo y Amplificación.

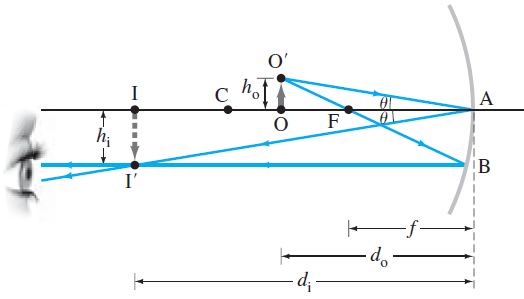
Es difícil dibujar ángulos pequeños para los rayos “paraxiales”. Para resultados más precisos, ahora se deducirá una ecuación que da la distancia de la imagen si se conocen la distancia del objeto y el radio de curvatura del espejo. Para hacer esto, consulte la siguiente figura.

La distancia del objeto, d_o, es la distancia del objeto (punto O) desde el centro del espejo. La distancia de la imagen, d_i, es la distancia de la imagen (punto I) desde el centro del espejo. La altura del objeto OO’ se llama h_o y la altura de la imagen, I’I, es h_i.

Se representan los dos rayos que salen de O’: O’FBI’ (igual que el rayo 2 en las figuras arriba vistas a, b, c)y O’AI’, que es un cuarto tipo de rayo que se refleja en el centro del espejo y que también sirve para encontrar un punto de imagen. El rayo O’AI’ obedece la ley de reflexión, de manera que los dos triángulos rectos O’AO e I’AI son similares. En consecuencia, se tiene:

Para el otro rayo que se ilustra, O’FBI’ los triángulos O’FO y ABF también son similares porque los ángulos son iguales y se usa la aproximación AB=h_i(espejo pequeño comparado con su radio). Más aún, FA = f, la distancia focal del espejo, de manera que:

Ahora se dividen ambos lados entre d_o y se reordenan para obtener:

Ésta es la ecuación que se buscaba. Se llama ecuación del espejo y relaciona las distancias del objeto y de la imagen con la distancia focal f (donde f = r/2).
La amplificación lateral, m, de un espejo se define como la altura de la imagen dividida entre la altura del objeto. A partir del primer conjunto de triángulos similares anteriores, se escribe:

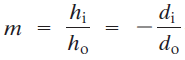
Ejemplo:

Imagen en un espejo cóncavo. Un anillo de diamantes de 1.50 cm
de alto se coloca a 20.0 cm de un espejo cóncavo con 30.0 cm de radio de curvatura. Determine:

1. la posición de la imagen y
2. su tamaño.

PLANTEAMIENTO Determine la distancia focal a partir del radio de curvatura (ecuación 1), f = r/2 = 15.0 cm. El diagrama de rayos es básicamente como el que se aprecia en la figura arriba mostrada, pues el objeto está entre F y C. La posición y el tamaño de la imagen se encuentran a partir de las ecuaciones 2 y 3.

SOLUCIÓN Al hacer referencia a la figura (c), se tiene CA = r = 30.0 cm,

FA = f = 15.0 cm y OA = d_o = 20.0 cm.

1) de acuerdo con la ecuación 2:

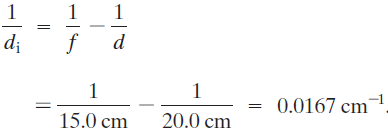
de manera que d_i =1/(0.0167cm^-1)=60cm puesto que d_i espositiva, la imagen está a 60 cm enfrente del espejo, en el mismo lado que el objeto.

2) a partir de la ecuación 3, la amplificación es:

La imagen es 3 veces mayor que el objeto y su altura es:

El signo menos, nos recuerda que la imagen esta invertida, como en aquella figura antes vista.

NOTA: Cuando un objeto está más lejos de un espejo cóncavo que el punto focal, se puede ver a partir de las figuras izquierda o derecha, que la imagen siempre está invertida y es real.

• 

• 

---

Espejos Convexos

El análisis usado para espejos cóncavos es aplicable a espejos convexos. Incluso la ecuación del espejo (ecuación 2) se sostiene para un espejo convexo, aunque las cantidades implicadas deben definirse cuidadosamente. La figura a) ilustra rayos paralelos que inciden sobre un espejo convexo. De nuevo, la aberración esférica será significativa, a menos que se suponga que el tamaño del espejo es muy pequeño comparado con su radio de curvatura. Los rayos reflejados divergen, pero parecen provenir del punto F detrás del espejo. Éste es el punto focal, y su distancia desde el centro del espejo (punto A) es la distancia focal, f. Es fácil demostrar que, de nuevo, f = r/2. Se ve que un objeto en el infinito produce una imagen virtual en un espejo convexo. De hecho, sin importar dónde se coloque el objeto en el lado reflectante de un espejo convexo, la imagen será virtual y derecha, como se indica en la figura b).
Para encontrar la imagen, dibuje los rayos 1 y 3 de acuerdo con las reglas usadas antes en el espejo cóncavo, como se muestra en la figura figura b). Note que, aunque los rayos 1 y 3 en realidad no pasan a través de los puntos F y C, la línea a lo largo de la cual se dibuja cada uno sí lo hace (se representa punteada). La ecuación del espejo, ecuación 32-2, se cumple para espejos convexos; sin embargo, la distancia focal f es negativa al igual que el radio de curvatura.

Ejemplos:

Espejo retrovisor convexo. Un espejo retrovisor externo en un automóvil es convexo, con un radio de curvatura de 16.0 m (figura). Determine la ubicación de la imagen y su amplificación para un objeto a 10.0 m del espejo.

PLANTEAMIENTO Se siguen explícitamente los pasos de la estrategia de Resolución de problemas.
SOLUCIÓN

1. Dibuje un diagrama de rayos. El diagrama de rayos será como el de la figura b, pero la gran distancia del objeto (d_o = 10.0 m) hace difícil un dibujo preciso. Se tiene un espejo convexo, de manera que r es negativo por convención.

2. Ecuaciones de espejo y amplificación. El centro de curvatura de un espejo convexo está detrás del espejo, como lo está su punto focal, así que se establece que r = -16.0 m, de manera que la distancia focal es f = r/2 = -8.0 m. El objeto está enfrente del espejo, d_o = 10.0 m. Al despejar 1/d_i en la ecuación del espejo, ecuación 2, se obtiene:

3. Convenciones de signos. La distancia de la imagen es negativa, -4.4 m, así que la imagen está detrás del espejo. La amplificación es m=+0.44, así que la imagen está derecha (misma orientación que el objeto) y tiene menos de la mitad de la altura que el objeto.

4. Comprobación. Los resultados son congruentes con la figura b.

Los espejos retrovisores convexos de los vehículos a veces vienen con una advertencia de que los objetos están más cerca de lo que parecen en el espejo. El hecho de que d_i pueda ser menor que d_o (como en la imagen del retrovisor) parece contradecir esta observación. La verdadera razón por la que los objetos parecen más alejados es que su
imagen en el espejo convexo es más pequeña de lo que sería en un espejo plano, y la distancia de los objetos ordinarios, como la de los otros automóviles, se juzga principalmente por su tamaño.

---

Ejercicios

1.- Un espejo esférico cóncavo tiene un radio de curvatura de 1.5 m. Determinar:

a) la posición.

b) la altura de la imagen de un objeto real de 10 cm de altura, situado delante de un espejo a una distancia de 1 m.

NOTA: como el espejo es Cóncavo, su radio de curvatura es negativo(-1)

---

2.-Un objeto de 10 cm está colocado a 20 cm delante de un espejo de distancia focal 10 cm. Determinar, Nota: la distancia focal es positiva, por lo tanto…

a) tipo de lente

b) posición de la imagen

c) aumento lateral