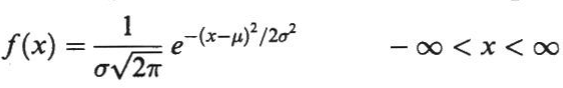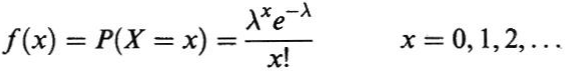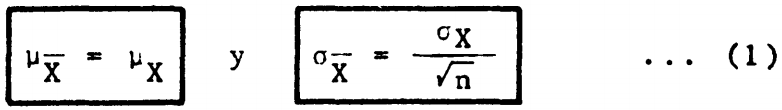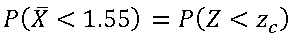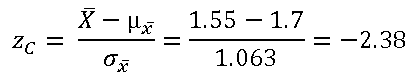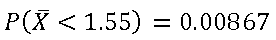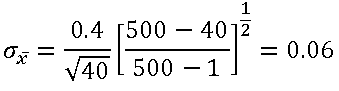En Estadística se le llama Inferencia al Proceso de Inducir o Deducir las características o parámetros poblacionales a partir de la información muestral, midiendo con probabilidades la incertidumbre inherente.
Lo anterior se puede realizar ya sea como un valor puntual, como un intervalo, o bien, establecer valores hipotéticos de los parámetros y probar estadísticamente si son válidas las hipótesis. A los primeros dos casos se les conoce como Estimación estadística puntual o por intervalos y a los segundos, Prueba de hipótesis.
La Distribución Normal
Uno de los ejemplos más importantes de una distribución de probabilidad continua es la distribución normal, llamada a veces la distribución gaussiana. La función de densidad para esta distribución está dada por
donde µ y σ son la media y deviación estándar respectivamente.
si X tiene la función de Distribución, decimos que la variable aleatoria X está distribuida normalmente con media µ y varianza σ2. Sea Z la variable estandarizada correspondiente a X, tenemos:
Distribución de Poisson
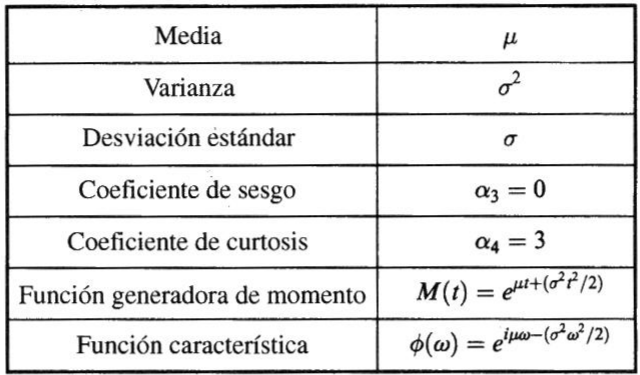
Sea X una variable aleatoria discreta que puede tomar los valores 0,1,2,… tal que la Función de probabilidad de X esta dada por:
donde λ es una constante positiva dada, esta distribución se llama La Distribución de Poisson(por S.D. Poisson),y la variable aleatoria que tiene esta distribución se dice que esta distribuida según Poisson.
Distribución t de Student
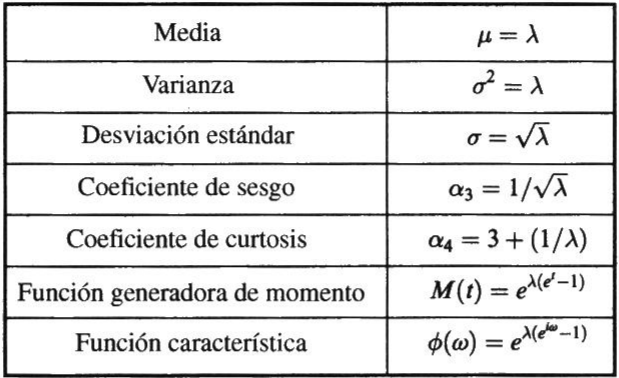
Si una variable aleatoria tiene función de densidad
se dice que tiene distribución t de Student o Distribución t, con v grados de libertad. Si v es grande(v≥30), la gráfica de f(t) se aproxima muy de cerca a la curva normal estándar; la distribución de t, es simétrica.
Ejemplo de Distribución Normal
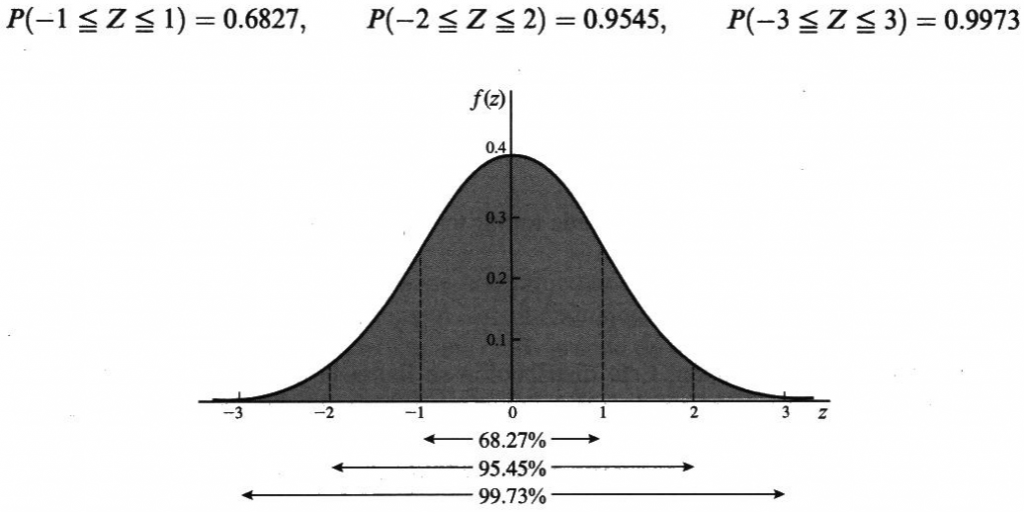
Encuentre el área bajo la curva normal estándar que aparecen en las sombras de los rangos propuestos:
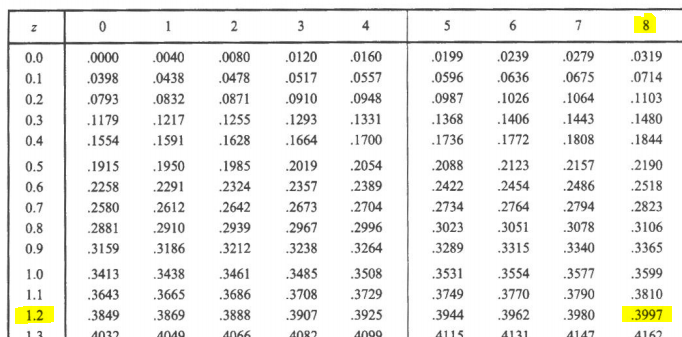
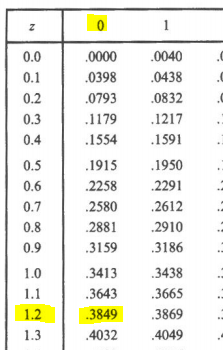
- entre z=0 y z=1.2
- entre z=-0.68 y z=0
- entre z=-0.46 y z=2.21
- entre z=0.81 y z=1.94
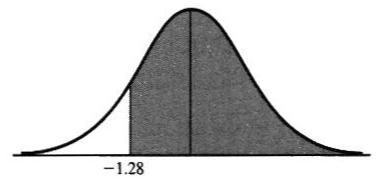
- a la derecha de z=-1.28

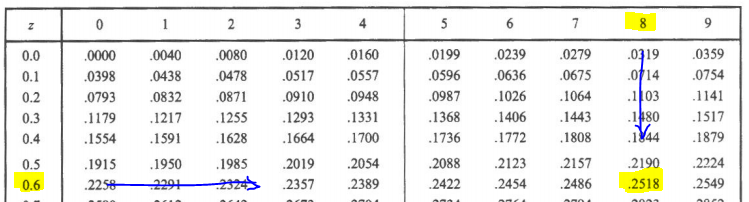
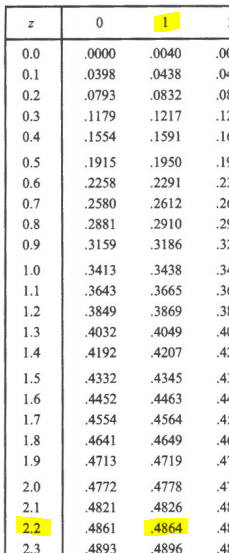
1) En el Documento con la tabla de las áreas bajo la curva normal estándar, desplazarse por la columna z hasta 1.2, luego en la columna 0, nos da el resultado:
2) el área requerida = area entre z=0 y z=+0.68(por simetría), por lo que el resultado sería 0.2518
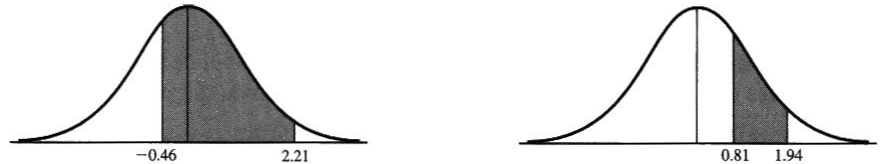
3) Área requerida = (área entre z=-0.46 y z=0)+(área entre z=0 y z=2.21)
(área entre z=+0.46(simetría) y z=0)+(área entre z=0 y z=2.21)
+
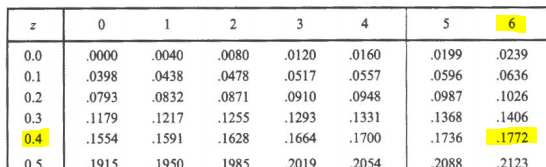
z=0.17720 + 0.4864 = 0.6636
El área 0.6636, representa la probabilidad de que Z esté entre -0.46 y 2.21
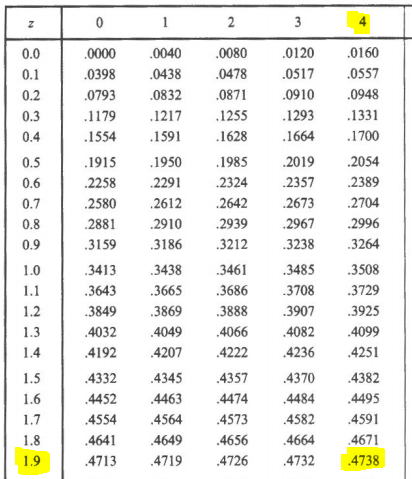
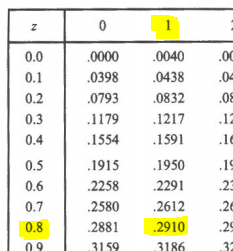
4) Área requerida = (área entre z=0 y z=1.94) – (área entre z=0 y z=0.81)
–
z=0.4738 – 0.2910 = 0.1828
5) Área requerida = (área entre z=-1.28 y z=0) + (área a la derecha de z=0)
+
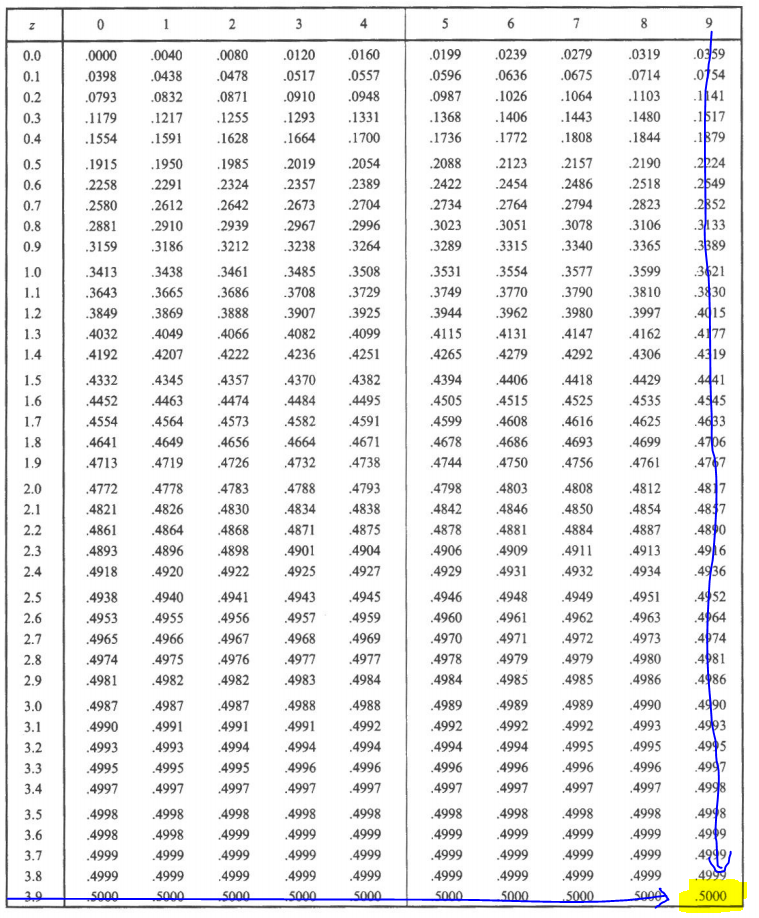
z=0.3997 + 0.5 = 0.8997
Distribuciones Muestrales
Un Estadístico muestral es una variable aleatoria que está en función de uno o más elementos de la muestra: la media, desviación estándar, varianza son ejemplo de medidas descriptivas.
Ejemplo 1:
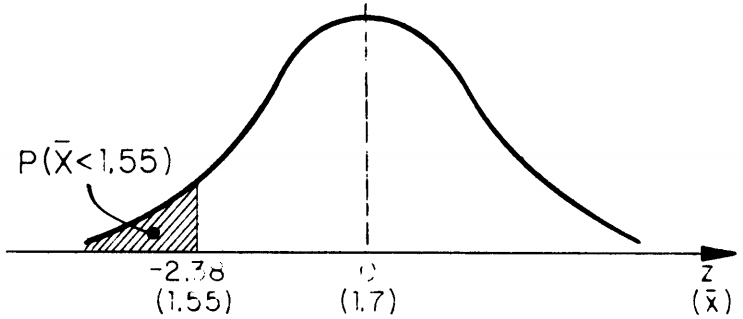
El peso promedio de los melones de una huerta es de 1.7 Kg, con una desviación estándar de 0.4 Kg. ¿Cuál es la probabilidad de que un posible comprador tome una muestra aleatoria de 40 unidades y encuentre que el peso promedio de la muestra es menor a 1.55 Kg?
Solución:
En este caso la variable aleatoria es el peso promedio de la muestra y las expresiones en 1:
con lo cual:
donde:
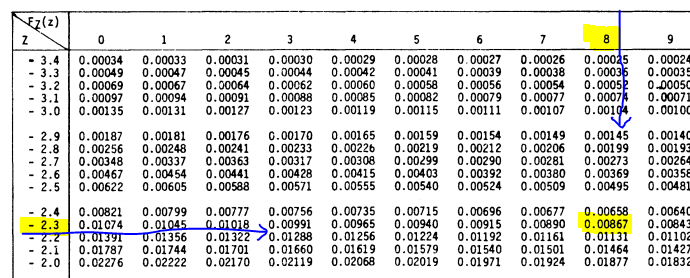
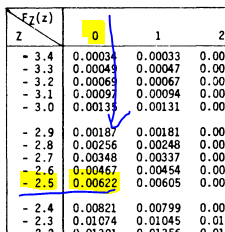
Buscando en la Tabla de «Función de Distribución acumulada de la distribución normal estándar», tenemos:
Esta probabilidad se muestra en la siguiente figura:
Cuando la Población es Finita y la selección de muestras se hace sin reemplazar las unidades observadas, la Desviación estándar se altera ligeramente, para reducir esta alteración se debe multiplicar la Desviación estándar por el Factor.
donde, N es el tamaño de la Población.
Ejemplo 2:
Considerando el ejemplo 1, ¿Cuál es la probabilidad de que el peso promedio sea menor a 1.55 Kg, si el muestreo se efectúa sin reemplazo, y en la Huerta solo se tienen únicamente 500 melones?
Solución:
Como la Población es finita(N=500) y n=40, de las expresiones (1) y (2):
con lo cual:
Por lo tanto(revisando la tabla de probabilidades):