Circuitos en serie
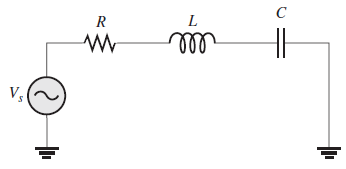
La reactancia inductiva (XL) causa que la corriente total se retrase con respecto al voltaje aplicado. La reactancia capacitiva (XC) tiene el efecto opuesto: provoca que la corriente se adelante con respecto al voltaje. Por tanto, XL y XC tienden a contrarrestarse entre sí. Cuando son iguales, se eliminan y la reactancia total es de cero.
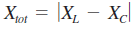
El valor absoluto de la diferencia de las dos reactancias se considera positivo sin que importe cuál reactancia sea más grande.Por ejemplo, 3 – 7 = -4, pero el valor absoluto es |3 – 7| = 4
La impedancia total del circuito RLC se establece en forma rectangular en la ecuación:
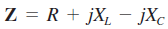
y en forma polar en la ecuación:
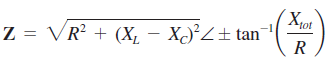
En esta última ecuación la raiz es la magnitud y tangente el ángulo de fase, Si el circuito es predominantemente inductivo, el ángulo de fase es positivo; y si es predominantemente capacitivo, el ángulo de fase es negativo.
Ejemplo 1:
Para el circuito RLC en serie de la siguiente figura, determine la impedancia total. Exprésela en forma tanto rectangular como polar:
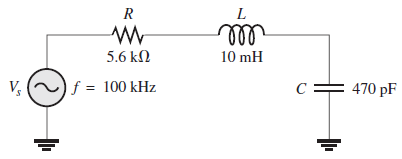
Solución: Primero, determine XC y XL:
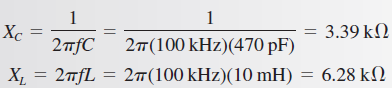
En este caso, XL es mayor que XC, y por tanto el circuito es más inductivo que capacitivo. La magnitud de la reactancia total es

La impedancia en forma rectangular es:

La impedancia en forma polar es:
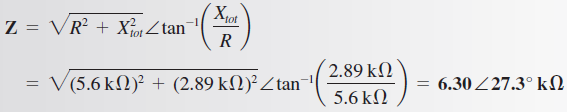
El ángulo positivo indica que el circuito es inductivo.
Ejemplo 2:
Con cada una de las siguientes frecuencias de entrada, encuentre la impedancia en forma polar para el siguiente circuito. Observe los cambios en magnitud y ángulo de fase con la frecuencia.

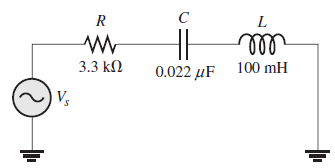
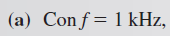
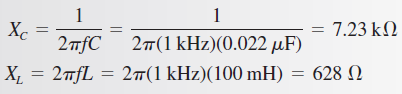
El circuito es claramente capacitivo, y la impedancia es:
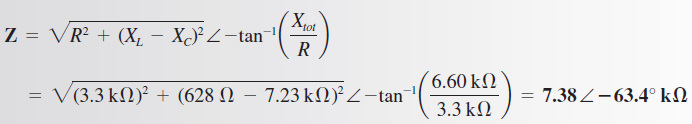
El signo negativo del ángulo se utiliza para indicar que el circuito es capacitivo.
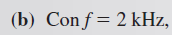
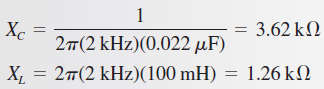
El circuito sigue siendo capacitivo, y la impedancia es
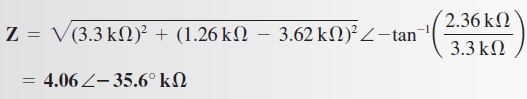
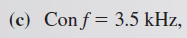

El circuito es casi puramente resistivo porque XC y XL son casi iguales, pero es un poco inductivo. La impedancia es


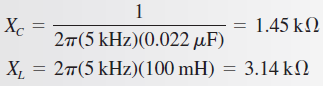
Ahora el circuito es predominantemente inductivo. La impedancia es
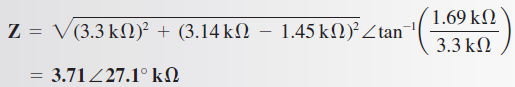
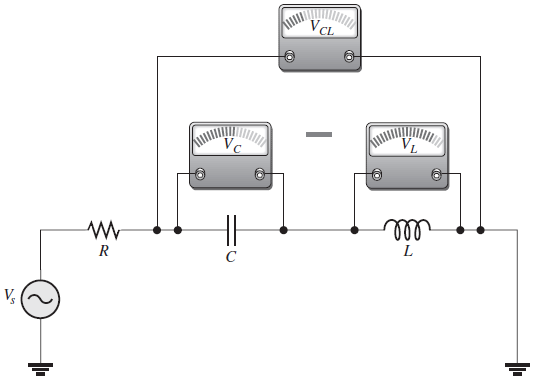
En un circuito RLC en serie, el voltaje entre las terminales del capacitor y entre las terminales del inductor siempre están desfasados entre sí por 180°. Por esa razón, VC y VL se restan entre sí, y por tanto el voltaje de L y C combinados siempre es menor que el voltaje individual más grande que pueda haber entre las terminales de uno u otro componente, tal como ilustra a continuación.
y el diagrama de forma de onda:
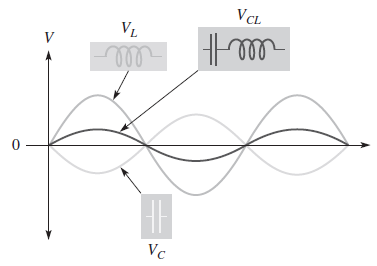
VCL es la suma algebraica de VL y VC. Debido a la relación de fase, VL y VC efectivamente se restan.
Ejemplo 3:
Determine la corriente y los voltajes de cada componente mostrado a continuación. Exprese cada cantidad en forma polar y trace un diagrama fasorial completo de los voltajes.
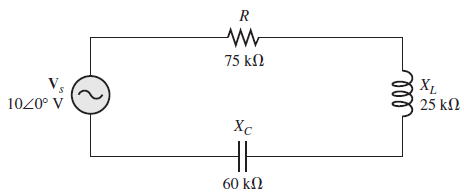
Solución, Primero determine la impedancia total.
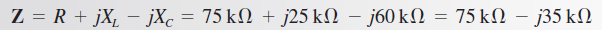
Por conveniencia, convierta a forma polar aplicando la ley de Ohm.
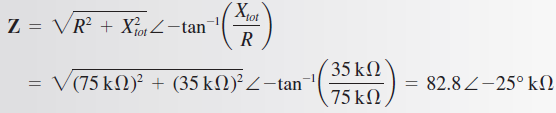
donde Xtot = | XL – XC |
Aplique la ley de Ohm para determinar la corriente
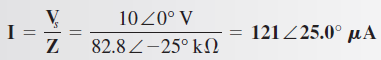
Ahora, aplique la ley de Ohm para determinar los voltajes entre las terminales de R, L y C.
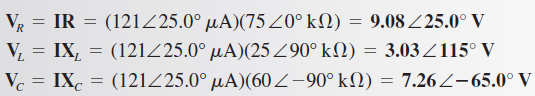
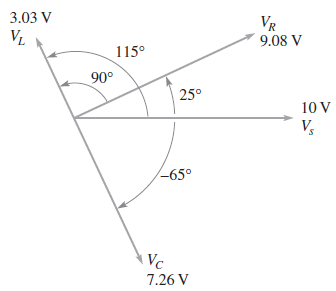
El diagrama fasorial aparece en la siguiente figura. Las magnitudes representan valores rms. Observe que VL adelanta en 90° a VR, y VC está retrasado 90° con respecto a VR. Asimismo, existe una diferencia de fase de 180° entre VL y VC. Si el fasor de corriente se mostrara, aparecería con el mismo ángulo que VR. La corriente adelanta en 25° a Vs, que es el voltaje de fuente, lo cual indica la presencia de un circuito capacitivo (XC > XL). El diagrama fasorial gira 25° a partir de su posición usual porque la referencia es el voltaje de fuente, Vs, el cual se muestra orientado a lo largo del eje x.
Ejercicio 1:
Determine Z en forma polar con f = 7 kHz.(del ejemplo 2)
Ejercicio 2:
Los siguientes voltajes ocurren en cierto circuito RLC en serie. Determine el voltaje de fuente:
VR= 24 ∠ 30° V,
VL = 15 < 120° V,
VC = 45 < -60° V.
Circuitos en paralelo
El siguiente circuito RLC dispuesto en paralelo. La impedancia total se calcula utilizando el método del recíproco de la suma de recíprocos, exactamente como se hizo para circuitos con resistores en paralelo.
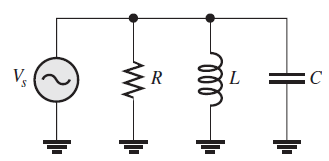
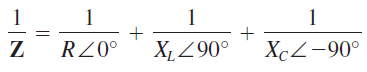
o
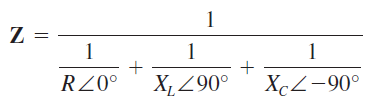
Ejemplo 1:
Determine Z en forma polar para el circuito RLC en paralelo de la siguiente figura
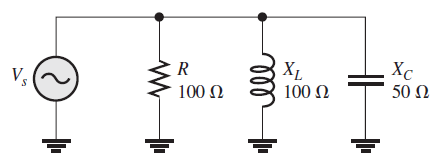
Solución: Use la fórmula de la suma de recíprocos
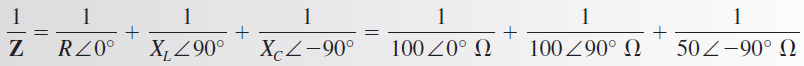
Aplique la regla para la división de números polares.
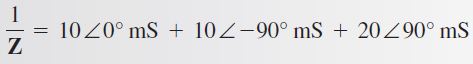
Recuerde que en el denominador el signo del ángulo cambia cuando se divide. A continuación, convierta cada término en su equivalente rectangular y combine:
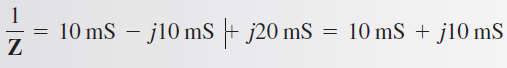
Tome el recíproco para obtener Z y luego convierta a forma polar
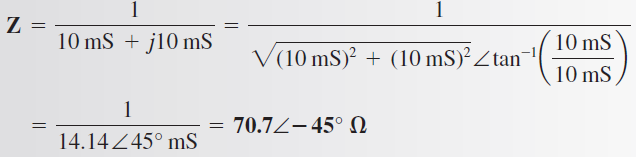
El ángulo negativo indica que el circuito es capacitivo. Esto puede resultar sorpresivo porque XL > XC. Sin embargo, en un circuito en paralelo, la cantidad más pequeña tiene el efecto más grande en la corriente total porque su corriente es máxima. Similar al caso de resistencias en paralelo, la reactancia menor atrae más corriente y tiene el mayor efecto en la Z total. En este circuito, la corriente total adelanta en 45° al voltaje total.
Conductancia, susceptancia y admitancia
Los conceptos de conductancia (G), susceptancia capacitiva (BC), susceptancia inductiva (BL), y admitancia (Y). Las fórmulas fasoriales se vuelven a establecer aquí.
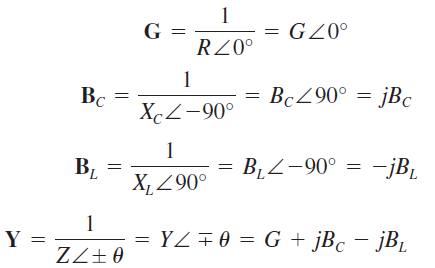
La unidad de medida para estas cantidades es el siemens (S).
Ejemplo 2:
Para el siguiente circuito RLC, determine la conductancia, la susceptancia capacitiva, la susceptancia inductiva, y la admitancia total. También, encuentre la impedancia.
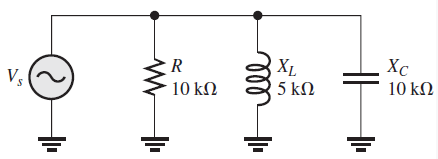
Solución
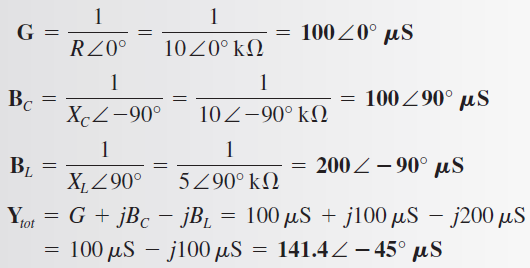
A partir de Ytot, es posible determinar Ztot
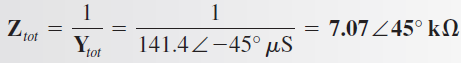
Relaciones de corriente
En un circuito RLC dispuesto en paralelo, las corrientes que circulan por las ramas capacitiva e inductiva siempre están desfasadas en 180° entre sí (omitiendo cualquier resistencia de bobina). Como IC e IL se suman algebraicamente, la corriente total es en realidad la diferencia de sus magnitudes. Por tanto, la corriente total que entra a las ramas de L y C en paralelo siempre es menor que la corriente de rama individual más grande, como ilustra la siguiente figura y el diagrama de forma de onda de la figura posterior. Desde luego, la corriente que circula en la rama resistiva siempre está desfasada en 90° con respecto a ambas corrientes reactivas, según muestra el diagrama fasorial de la figura 17-24.
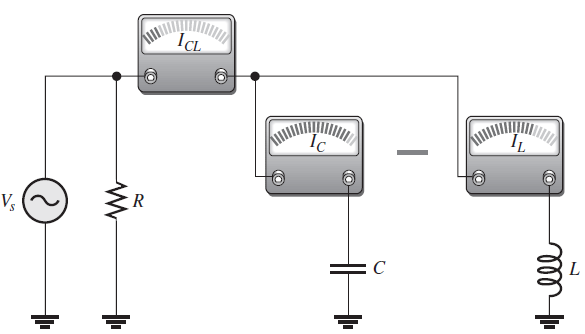
La corriente total que fluye por la combinación en paralelo de C y L es la diferencia de las dos corrientes de rama.
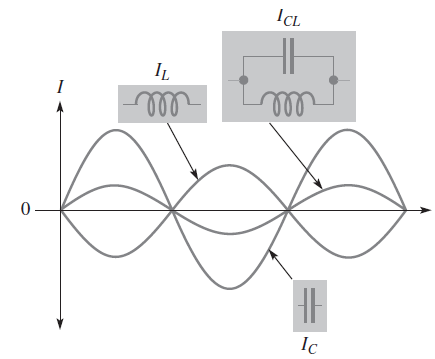
IC y IL se restan efectivamente
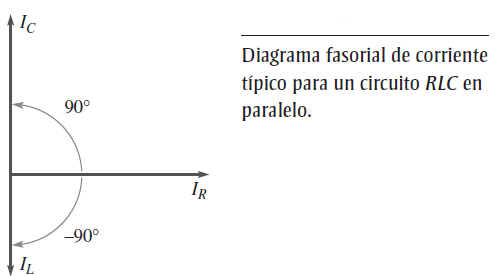
La corriente total se expresa como
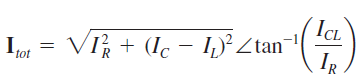
donde ICL es IC – IL, la corriente total que fluye por las ramas L y C.
Ejemplo 2:
Para el circuito de la siguiente figura, determine cada corriente de rama y la corriente total. Trace un diagrama de su relación
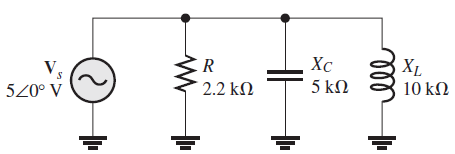
Solución Use la ley de Ohm para determinar cada corriente de rama en forma fasorial

La corriente total es la suma fasorial de las corrientes de rama. Según la ley de Kirchhoff

Al convertir a forma polar se obtiene

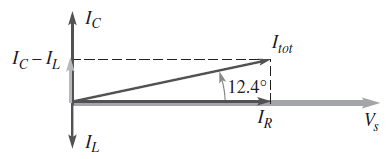
La corriente total es de 2.32 mA adelantada en 12.4° a Vs. La siguiente figura es el diagrama fasorial de corriente para el circuito.
Ejercicio 1:
Determine la admitancia de un circuito en paralelo en el cual R = 1.0 kΩ, XC = 500 Ω, y
XL = 1.2 kΩ.
Ejercicio 2:
En un circuito de tres ramas dispuesto en paralelo,
R = 150 Ω,
XC = 100 Ω,
XL = 50 Ω.
Determine la corriente en cada rama cuando Vs = 12 V.
Circuitos en serie-paralelo
Los dos ejemplos siguientes ilustran un acercamiento al análisis de circuitos con combinaciones en serie como en paralelo de resistencia, inductancia y capacitancia
Ejemplo 1:
En la siguiente figura, determine el voltaje entre las terminales del capacitor en forma polar. ¿Es este circuito predominantemente inductivo o predominantemente capacitivo?
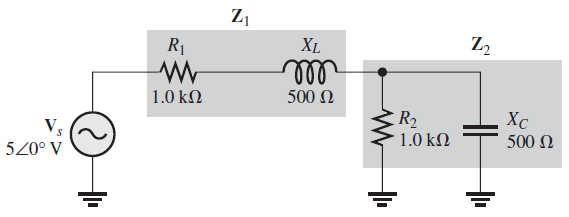
Solución, En este análisis, use la fórmula del divisor de voltaje. La impedancia de la combinación en serie de R1 y XL se llama Z1. En forma rectangular:

Al convertir a forma polar se obtiene:

La impedancia de la combinación en paralelo de R2 y XC se llama Z2. En forma polar:

Al convertir a forma rectangular se obtiene:
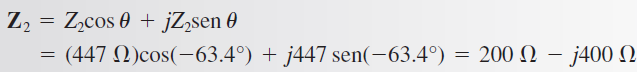
La impedancia total Ztot en forma rectangular es

Al convertir a forma polar se obtiene

Ahora aplique la fórmula del divisor de voltaje para obtener VC
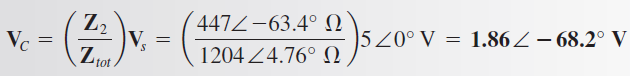
Por consiguiente, VC es de 1.86 V y está retrasado en 68.2° con respecto a Vs. El término +j en Ztot, o el ángulo positivo en su forma polar, indica que el circuito es más inductivo que capacitivo. No obstante, es sólo un poco más inductivo porque el ángulo es pequeño. Este resultado puede sorprendernos, porque XC = XL = 500 Ω. Sin embargo, el capacitor está en paralelo con un resistor, así que en realidad el efecto del capacitor en la impedancia total es menor que el del inductor. La siguiente figura muestra la relación fasorial de VC y Vs. Aunque XC = XL, este circuito no está en condición de resonancia porque el término j de la impedancia total no es de cero debido a la combinación en paralelo de R2 y XC. Esto queda de manifiesto al observar que el ángulo de fase asociado con Ztot es de 4.76° y no de cero

Ejemplo 2:
Para el circuito reactivo siguiente, encuentre el voltaje en el punto B con respecto a tierra:

Solución: El voltaje (VB) en el punto B es el voltaje entre las terminales de salida abiertas. Use el método del divisor de voltaje. Para ello, primero debe conocer el voltaje (VA) en el punto A; por lo que es necesario determinar la impedancia desde el punto A hasta tierra como un punto de partida. La combinación en paralelo de XL y R2 está en serie con XC2. Esta combinación está en paralelo con R1. Llamemos a ZA la impedancia desde el punto A hasta tierra. Para determinar ZA, siga los siguientes pasos. La impedancia de la combinación en paralelo de R2 y XL se designa como Z1.

A continuación, combine Z1 en serie con XC2 para obtener la impedancia Z2.

Al convertir a forma polar se obtiene

Por último, combine Z2 y R1 en paralelo para obtener ZA.

El circuito simplificado se muestra a continuación:

A continuación, use el principio del divisor de voltaje para determinar (VA) en el punto A en el diagrama principal. La impedancia total es:

Al convertir a forma polar se obtiene

El voltaje en el punto A es

En seguida, calcule el voltaje (VB) en el punto B dividiendo VA, como se indica en el primer circuito. VB es el voltaje de salida en la terminal abierta

sobresale que, VA es más grande que Vs y VB es más grande que VA. Este resultado es posible gracias a la relación de desfase de los voltajes reactivos. Recuerde que XC y XL tienden a eliminarse entre sí.

Conversión de en serie-paralelo a paralelo
La configuración particular en serie-paralelo mostrada en la siguiente figura es importante porque representa un circuito que tiene ramas L y C en paralelo, con la resistencia de devanado de la bobina tomada en cuenta como resistencia en serie en la rama L.

Es conveniente ver al circuito en serie-paralelo del circuito anterior en una forma equivalente en paralelo, como a continuación para mejor entendimiento:
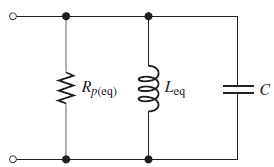
Las fórmulas siguientes proporcionan la inductancia equivalente, Leq, y la resistencia en paralelo equivalente, Rp(eq):

donde Q es el factor de calidad de la bobina, XL/RW. Las derivaciones de estas fórmulas son bastante complicadas, y por tanto no se muestran aquí. Advierta en las ecuaciones que, con Q ≧ 10, el valor de Leq es aproximadamente el mismo que el valor original de L. Por ejemplo, si L=10 mH y Q = 10, entonces

La equivalencia de los circuitos significa que, a una frecuencia dada, cuando se aplica el mismo valor de voltaje a ambos circuitos, la misma corriente total fluye en ambos circuitos y los ángulos de fase son los mismos. De manera básica, un circuito equivalente sólo propicia que el análisis de circuitos sea más conveniente
Ejemplo 3:
Convierta el siguiente circuito serie-paralelo en una forma equivalente dispuesta en paralelo a la frecuencia dada.

Solución: Determine la reactancia inductiva

El factor Q de la bobina es

Como Q > 10, entonces Leq > L = 5 mH. La resistencia equivalente en paralelo es

Esta resistencia equivalente aparece en paralelo con R1 como se muestra en la siguiente figura(a). Cuando se combinan, resulta una resistencia total en paralelo (Rp(tot)) de 3.2 k Ω, como indica la figura en (b).


Ejercicio:
Cierto circuito resonante tiene un inductor de 100 µH con resistencia de devanado de 2 Ω en paralelo con un capacitor de 0.22 µF. Si Q = 8, determine el equivalente en paralelo de este circuito.
Instrucciones:
Desarrollar y resolver los ejercicios propuestos, una vez resultos, fotografiar/escanear y enviar sus resultados al correo lsaucedoh@utrng.edu.mx