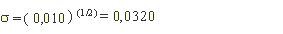Fases y problemas del proceso estadístico
Podemos distinguir tres fases en el proceso estadístico:
- Muestreo: selección de la muestra que se analizará.
- Estadística Descriptiva: análisis particular de los datos de la muestra seleccionada.
- Inferencia Estadística: estudio de la posible generalización de los resultados obtenidos en la muestra al global de la población
Población: es el objeto del estudio.
Muestra: Sobre la población que se va a estudiar se toma un cierto carácter o rasgo que dará lugar a una variable, denótese por X, y que la población suele ser demasiado grande. Ello nos obliga a contentarnos con estudiar el carácter o rasgo sobre un subconjunto de n individuos de la población. La letra n queda reservada para denotar el tamaño de muestra.
En un sentido muy amplio, la Estadística Descriptiva es la parte o fase de la Estadística dedicada a la descripción de un conjunto de n datos,
Tablas de frecuencias
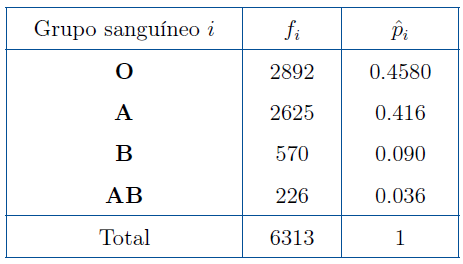
Son la fase preliminar de cualquier estudio descriptivo, utilizándose como medio para la elaboración de gráficos y el cálculo de valores típicos. Ejemplo 1. En estudio sobre el grupo sanguíneo realizado con n = 6313 individuos se
obtuvo la siguiente tabla de frecuencias:
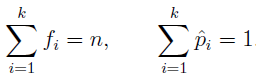
Medidas de centralización
Media aritmética: es el valor central en sentido aritmético. Se obtiene sumando los n datos de la muestra y dividiéndolos por el tamaño de ésta:
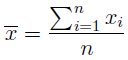
Mediana: es el valor central x en el sentido del orden, es decir, aquel que quedaría en el medio una vez ordenados los datos de menor a mayor, repitiéndose si es necesario tantas veces como aparezcan en la muestra. Si el número de datos n es impar no cabe duda de que la mediana es el dato que ocupa la posición n+1/2 . Si n es par tenemos un conflicto que puede resolverse mediante un convenio: definir la mediana como la semisuma de los datos que ocupen las posiciones n/2 y n/2 + 1.
Medidas de dispersión
Rango: expresa la diferencia entre el valor mayor y el menor.
Varianza: nos da una medida de dispersión relativa al tamaño muestral.
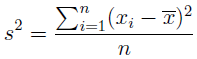
Desviación típica o estándar: la raíz cuadrada de la varianza.
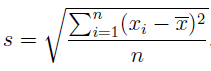
Ejemplo:
Medimos la altura de los niños de una clase y obtenemos los siguientes resultados :
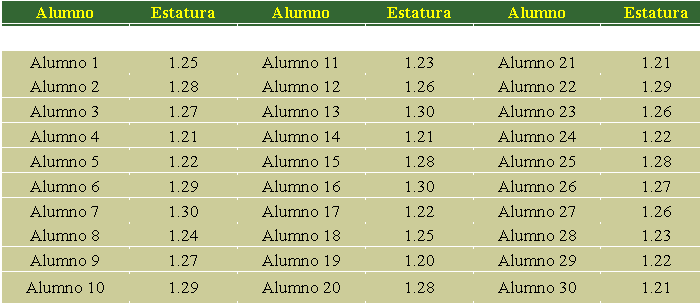
Si se presenta la información de manera estructurada, tenemos la siguiente tabla de frecuencias:
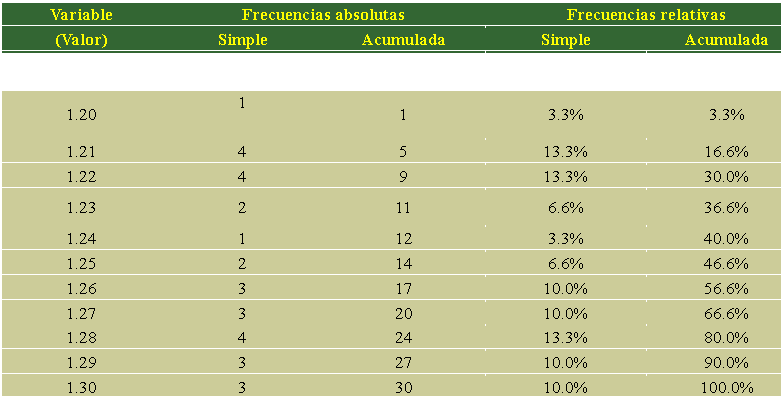
- Media aritmética
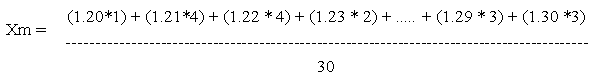
Entonces se tiene que: Xm = 1.253, Por lo tanto, la estatura media de este grupo de alumnos es de 1.253
- Mediana
La mediana de esta muestra es 1.26 m, ya que por debajo está el 50% de los valores y por arriba el otro 50%. Esto se puede ver al analizar la columna de frecuencias relativas acumuladas.
- Moda
Hay 3 valores que se repiten en 4 ocasiones: el 1.21, el 1.22 y el 1.28, por lo tanto esta seria cuenta con 3 modas.
- Varianza
Mide la distancia existente entre los valores de la serie y la media. Se calcula como sumatoria de las diferencias al cuadrado entre cada valor y la media, multiplicadas por el número de veces que se ha repetido cada valor. El sumatorio obtenido se divide por el tamaño de la muestra.
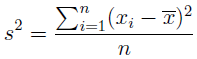
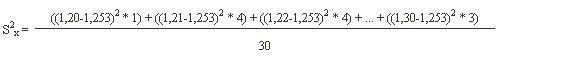
Por lo tanto, la varianza es 0.010
- Desviación típica
es la raíz cuadrada de la varianza: