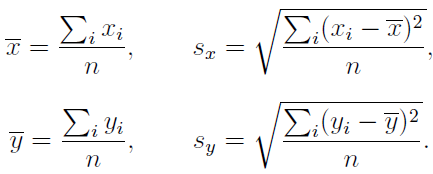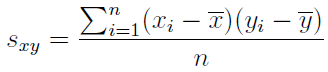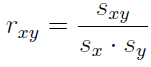La media y desviación típica(estándar)
Ejemplo. Se indica a continuación el peso, X, (kg) y la estatura, Y , (cm) de 12 personas:

En el Ejemplo anterior, se tiene:
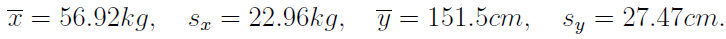
Para calcular un valor típico que exprese el grado de relación (o correlación) lineal entre ambas variables en la muestra, diferente a los resultados obtenidos, éstos se deben conjugar.
Covarianza: la covarianza muestral es una primera medida del grado de correlación y se define mediante:
La covarianza, en el caso del Ejemplo anterior se expresará en kg.cm, puede ser tanto positiva como negativa, pero puede probarse que debe estar comprendida entre los siguientes valores:
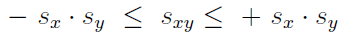
sxy debe estar comprendida entre -630.71 y 630.71. A través del programa estadístico obtenemos su valor concreto en este caso, que es sxy = 577:86 kg.cm.
Coeficiente de correlación lineal de Pearson: supone una medida adimensional de grado de correlación lineal observado en la muestra y se define como sigue:
Este parámetro, que se denota normalmente de forma simplificada por r, se interpreta en los mismos términos que la covarianza con la salvedad de que se encuentra en todo caso entre -1 y 1 y alcanza esos valores cuando se da en la muestra una correlación lineal perfecta, bien sea inversa o directa, respectivamente. La proximidad a 0 indica que en la muestra se observa escasa correlación lineal. Así, los datos del Ejemplo corresponden a r = 0.916.