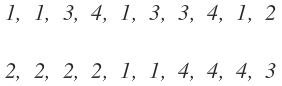Tablero Canvas -descripción
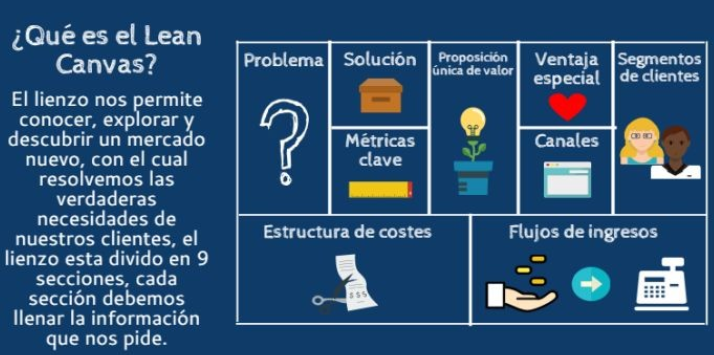
El modelo Canvas(habitualmente denominado Business Model Canvas) se trata de un lienzo para diseñar modelos de negocio
(más…)Ejercicio 1
Realizar una propuesta de proyecto redactando los aspectos que nos solicita un Tablero Canvas.
La sugerencia del proyecto es realizarlo en el Lenguaje de programación Python y como aplicación:
- Un editor de texto Sencillo
- Un Navegador Web sencillo
Sobre Riesgos
A continuación, algunas consideraciones para el trato de riesgos en el proyecto:
Categorías generales de riesgos en proyectos de TI:
- Riesgos de Mercado.
- Riesgos Financieros.
- Riesgos Tecnológicos.
- Riesgos de las Personas.
- Riesgos de Estructura/Procesos.
Ejercicios de Tablas de distribución
Ejercicio 1
En un grupo escolar se tienen las siguientes calificaciones:
79 77 55 81 89
72 83 58 80 83
94 71 79 90 83
70 75 73 91 68
82 71 82 84 92
Nos piden diseñar la tabla de distribución de frecuencias que resuma los datos de las calificaciones anteriores.
Ejercicio 2
En una escuela se toma la estatura de 36 estudiantes como los que siguen:
1.68 1.90 1.4 1.5 1.77 1.79
1.56 1.47 1.68 1.88 1.41 1.88
1.83 1.55 1.75 1.94 1.76 1.58
1.85 1.87 1.53 1.46 1.48 1.96
1.95 1.84 1.87 1.67 1.56 1.97
1.94 1.92 1.76 1.45 1.65 1.52
Realizar una tabla de frecuencias con datos agrupados en intervalos
Ejemplo del llenado de una tabla de Frecuencias
A continuación se crearán algunas Tablas de Frecuencias. La tabla de frecuencias es una tabla donde los datos estadísticos aparecen bien organizados, distribuidos según su frecuencia, es decir, según las veces que se repite en la muestra.
Ejemplo: En una urbanización se ha realizado una encuesta preguntando cuántos dormitorios tienen sus viviendas. Los resultados sobre el número de dormitorios por vivienda fueron los siguientes:
(más…)Sobre variables en estadística
Variable aleatoria: característica de interés asociada a cada uno de los elementos de la población o muestra considerada. Ejemplos: (a) la edad de cada estudiante; (b) el número de visitas diarias que recibe cada periódico en línea; (c) el factor de impacto de cada revista, etc.
Variable cualitativa o categórica: variable que categoriza o describe cualitativamente un elemento de la población. Suele ser de tipo alfanumérico, pero incluso en el caso en que sea numérica no tiene sentido usarla en operaciones aritméticas. Ejemplos: (a) el teléfono o el correo electrónico de un estudiante; (b) la dirección IP de un periódico en línea; (c) el ISSN de una revista, etc.
(más…)Ejercicios de variables estadísticas en representaciones gráficas
Basados en los ejemplos vistos en la publicación «Sobre variables en estadística«, realizar los siguientes Gráficos, los cuales pueden ser diseñados en una Hoja de Cálculo o en alguna otra herramienta que lo permita realizar:
Ejercicio 1
Realizar un diagrama de Pareto que visualice los datos de bajas de los estudiantes en una escuela, se tiene la siguiente información:
- Dificultad:20
- Preparación anterior:25
- Económicos: 32
- Familiares: 7
- Calidad: 14
- Otros: 5
Estadística Descriptiva
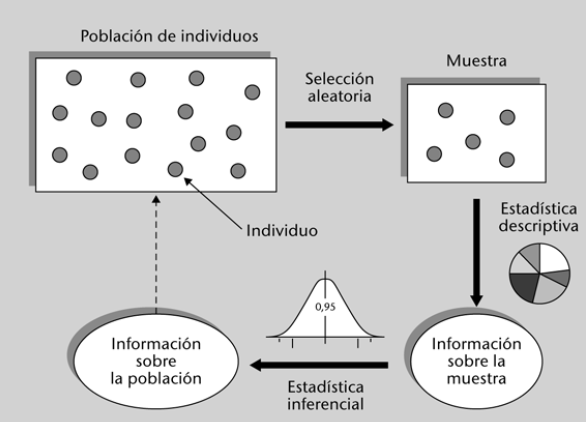
Para su estudio, la estadística se divide en: Estadística Descriptiva e Inferencia Estadística.
La Primera se encarga de la recopilación, organización, resumen y presentación de los datos numéricos obtenidos de la observación de un fenómeno; mientras que la Segunda tiene por objeto, obtener conclusiones probables sobre el comportamiento general del fenómeno, a partir de algunas observaciones particulares del mismo.
(más…)Ejercicios de Distribución de Poisson
Ejercicio 1
El recuento de leucocitos de un individuo sano puede presentar en promedio un valor mínimo de hasta 6000 por mm3 de sangre. Para detectar una deficiencia de leucocitos, se toma una gota de sangre de 0.001 mm3 y se halla el número X de leucocitos.
¿Cuántos leucocitos cabe esperar en un individuo sano? Si a lo sumo se encuentran dos, ¿hay signos de una deficiencia de leucocitos? Este experimento puede considerarse un proceso de Poisson. El suceso discreto de interés es encontrar un leucocito, el intervalo continuo es una gota de sangre. Sea el mm3 la unidad de medida; así, s = 0.001 y λ, la media de veces que tendremos un suceso por cada unidad, es 6000. Por lo tanto, X es una variable aleatoria de Poisson con P[X] = λ = 6000(0.001) = 6. Para una persona con buena salud, esperaríamos observar un promedio de, por lo menos, seis leucocitos. ¿Sería extraño encontrar dos células como máximo? ¿Lo expresaremos por P[ X ≤ 2 | λ = 6 ] ? R= 0.062
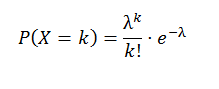
Ejercicio 2
En el estudio del sueño en los seres humanos se reconocen cinco fases (somnolencia, ligero, intermedio, profundo, REM) por medio del electroencefalograma. El sueño intermedio se caracteriza por la presencia de ondas de gran amplitud, que aparecen en un promedio de alrededor de dos ondas por segundo.
- ¿Cuál es la probabilidad de que, durante un sueño intermedio, no se presente ninguna de estas ondas durante un período de cinco segundos?
- ¿Cuál es la probabilidad de que aparezca un máximo de 15 de tales
- ondas en un período de cinco segundos?
- Si aparecieran 20 ó más de tales ondas durante un período de cinco segundos, ¿podría sospecharse que el sujeto no está en la etapa de sueño intermedio? Razonar sobre la base de la probabilidad implícita.
Instrucciones de entrega
Resolver en cualquier medio que les sea más cómodo(cuaderno, hoja blanca, word, excel, etc), en caso de hacerlo físicamente en hojas blancas o cuaderno, fotografiar o escanear.
Una vez resueltos los ejercicios, crear una carpeta con sus datos y comprimirla en rar o zip. P. ej.
Enviar al correo lsaucedoh@utrng.edu.mx
Ejercicios de Distribución Binomial
Ejercicio 1
Se va a construir una planta nuclear y se quiere conocer la opinión de los vecinos de la localidad. Se selecciona una muestra aleatoria de 20 individuos y se realiza un sondeo. Se piensa que el 60 % de los habitantes del lugar estará a favor del proyecto. Si esto es verdad, ¿cuántos piensa usted que expresarían una opinión favorable? Si sólo nueve o menos son de tal opinión, ¿piensa usted que es razón de peso para poner en duda la cifra 60 %? Explicarlo sobre la base de la probabilidad implícita.
Ejercicio 2
Para estudiar la regulación hormonal de una línea metabólica, se inyecta a ratas albinas un fármaco que inhibe la síntesis de proteínas del organismo. En general, 4 de cada 20 ratas mueren a causa del fármaco antes de que el experimento haya concluido. Si se trata a 10 animales con el fármaco, ¿cuál es la probabilidad de que al menos 8 lleguen vivos al final del experimento?
Instrucciones de entrega
Resolver en cualquier medio que les sea más cómodo(cuaderno, hoja blanca, word, excel, etc), en caso de hacerlo físicamente en hojas blancas o cuaderno, fotografiar o escanear.
Una vez resueltos los ejercicios, crear una carpeta con sus datos y comprimirla en rar o zip. P. ej.
Enviar al correo lsaucedoh@utrng.edu.mx