Variable aleatoria: característica de interés asociada a cada uno de los elementos de la población o muestra considerada. Ejemplos: (a) la edad de cada estudiante; (b) el número de visitas diarias que recibe cada periódico en línea; (c) el factor de impacto de cada revista, etc.
Variable cualitativa o categórica: variable que categoriza o describe cualitativamente un elemento de la población. Suele ser de tipo alfanumérico, pero incluso en el caso en que sea numérica no tiene sentido usarla en operaciones aritméticas. Ejemplos: (a) el teléfono o el correo electrónico de un estudiante; (b) la dirección IP de un periódico en línea; (c) el ISSN de una revista, etc.
Variable cuantitativa o numérica: variable que cuantifica alguna propiedad de un elemento de la población. Es posible realizar operaciones aritméticas con ella. Ejemplos: (a) el importe de la beca que recibe un estudiante; (b) los ingresos que genera un periódico en línea; (c) el número de revistas publicadas por una editorial, etc.
Variable cuantitativa discreta: variable cuantitativa que puede tomar un número finito o contable de valores distintos. Ejemplos: (a) edad de un estudiante; (b) número de enlaces a otras fuentes de información que ofrece un periódico en línea; (c) calificación que obtiene una revista en una escala entera de 1 a 5, etc.
Variable cuantitativa continua: variable cuantitativa que puede tomar
un número infinito (no contable) de valores distintos. Ejemplos: (a) altura o peso de un estudiante; (b) tiempo que transcurre entre la publicación de una encuesta en línea y el instante en que ya la han completado un centenar de internautas; (c) factor de impacto (sin redondear) de una revista, etc.
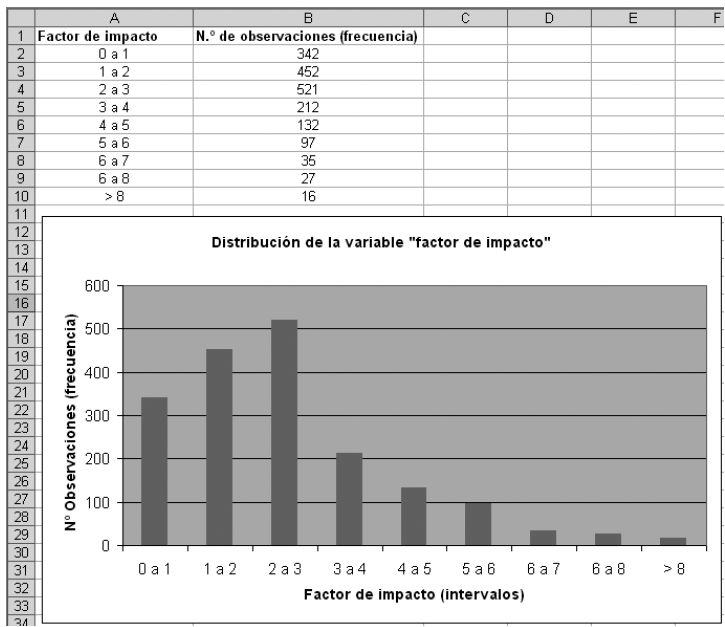
Distribución de una variable: en sentido amplio, una distribución es una tabla, gráfico o función matemática que explica cómo se comportan o distribuyen los valores de una variable, es decir, qué valores toma la variable así como la frecuencia de aparición de cada uno de ellos. Ejemplo: dada una muestra aleatoria de revistas, la distribución de la variable “factor de impacto de una revista” puede representarse mediante una tabla de frecuencias o mediante una gráfica como se observa a continuación, donde 342 de las revistas consideradas tienen un factor de impacto entre 0 y 1, 452 de las revistas tienen un factor de impacto entre 1 y 2, etc.
Descripción de datos mediante tablas y gráficos
Gráficos y tablas para datos cualitativos o categóricos
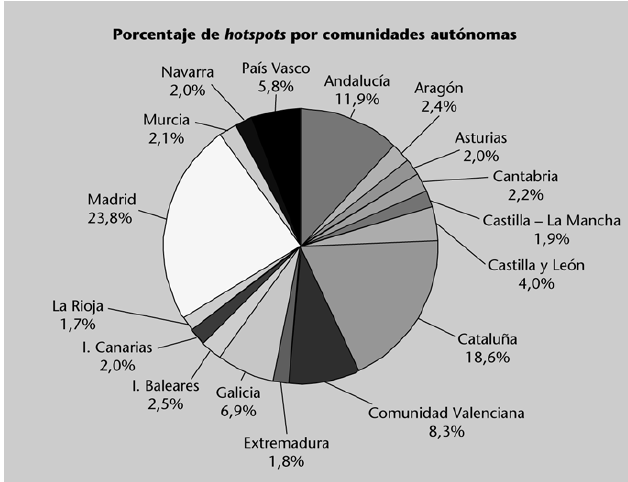
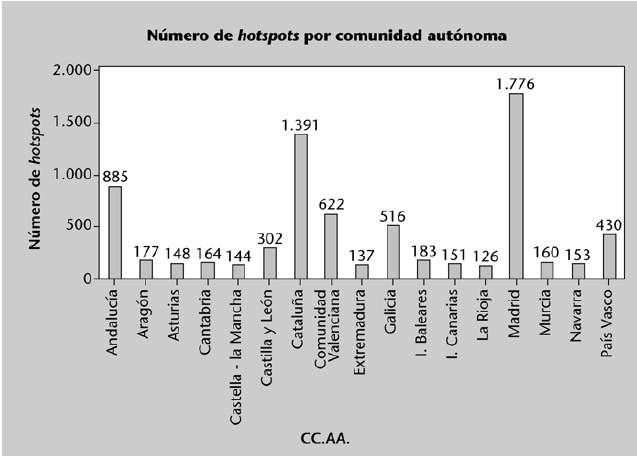
Pueden sintetizarse mediante una tabla que recoja, para cada categoría: el número de veces que aparece (frecuencia absoluta), el porcentaje de apariciones sobre el total de observaciones (frecuencia relativa), así como los acumulados de ambos valores. La siguiente tabla muestra esta información para la variable “número de hotspots (conexiones wi-fi) identificados en cada comunidad autónoma”.
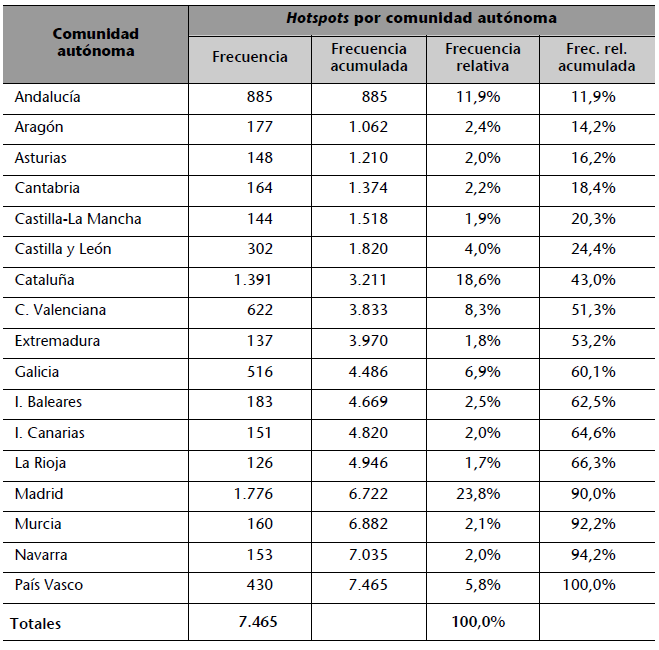
Suele ser habitual representar datos categóricos mediante el uso de gráficos circulares o bien mediante diagramas de barras.
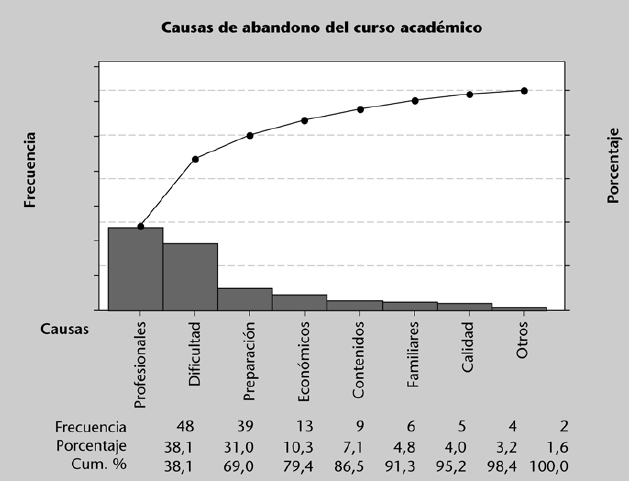
Un gráfico que también suele usarse bastante para describir datos cualitativos es el llamado diagrama de Pareto. Este gráfico está compuesto por: (a) un diagrama de barras en el que las categorías están ordenadas de mayor a menor frecuencia y (b) una línea que representa la frecuencia relativa acumulada
Los diagramas de Pareto son muy útiles para detectar cuándo un porcentaje reducido de categorías (p. ej.: un 20% de las categorías) “acapara” o representa un porcentaje alto de observaciones (p. ej.: un 80% de los datos). Suelen darse con frecuencia en contextos como los que siguen:
- Socioeconómicos. Un porcentaje reducido de los ciudadanos de un país acapara un alto porcentaje de la renta.
- Educativos. Un porcentaje reducido de causas generan la mayor parte de los abandonos del curso.
- Ingeniería de la calidad. Un alto porcentaje de fallos son debidos a un número muy reducido de causas
Gráficos y tablas para datos cuantitativos
Su representación gráfica o mediante tablas permite apreciar la forma de su distribución estadística, es decir, la forma en que se comporta la variable de interés (cuáles son los valores medios o centrales, cuáles son los valores más habituales, cómo varía, cómo de dispersos son los valores, si muestra algún patrón de comportamiento especial, etc.).
Uno de los gráficos más sencillos de elaborar es el llamado gráfico de puntos (dotplot). Se trata de un gráfico en el que cada punto representa una o más observaciones. Los puntos se apilan uno sobre otro cuando se repiten los valores observados.
Otro ejemplo de un gráfico de tallos.
El gráfico se ha construido a partir de una muestra de cincuenta calificaciones y que se ha usado una unidad de hoja (leaf) de 0,1. Esto significa que la segunda columna del gráfico representa la parte entera de la calificación, mientras que cada uno de los números situados a su derecha representa la parte decimal de una observación con dicha parte entera. Así, se pueden leer las siguientes calificaciones por orden de menor a mayor: 1,4,2,9,3,0,3,5,3,9,4,0, 4,3, etc.
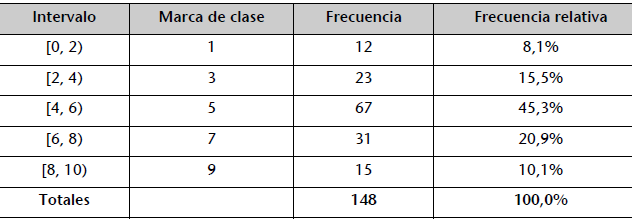
Ejemplo de tabla de frecuencias en el que se han agrupado los datos en intervalos. La frecuencia de cada intervalo viene determinada por el número de observaciones cuyos valores están en dicho intervalo. La marca de clase representa el valor medio del intervalo.
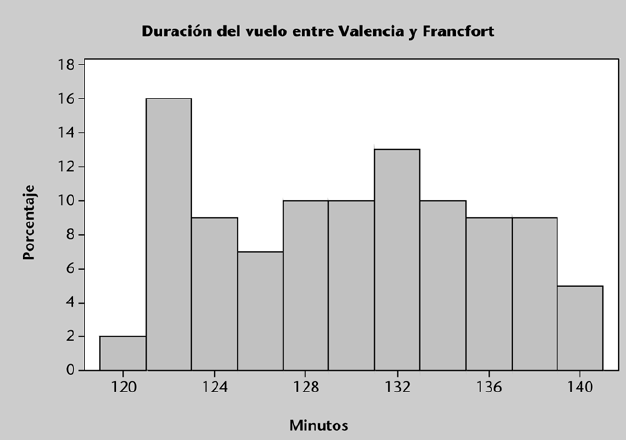
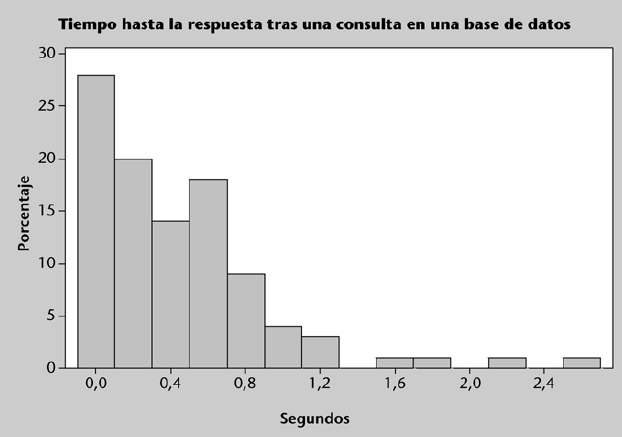
Un gráfico que utiliza también intervalos para agrupar los datos a representar es el histograma. El histograma muestra la frecuencia (absoluta o relativa) de cada clase, lo que permite visualizar de forma aproximada la distribución de los datos.

La figura anterior muestra un histograma con forma de campana: es una forma bastante simétrica, que presenta una mayor altura en la parte central y disminuye paulatinamente en las “colas” o extremos. Esta forma es bastante habitual y suele caracterizar el comportamiento de muchas variables (p. ej.: notas numéricas en un examen, peso o altura de individuos, temperaturas diarias, etc.). Sin embargo, también es habitual encontrarse con variables que muestran patrones de comportamientos completamente distintos.
La figura izquierda muestra un histograma en el que se aprecia una distribución más “uniforme” u homogénea de los datos, mientras que la figura de la derecha que le sigue muestra un histograma en el que se aprecia una distribución asimétrica o “sesgada” de los mismos.