Ya sabemos que los valores típicos estudiados anteriormente constituyen estimaciones o aproximaciones de los correspondientes parámetros poblacionales, que serán más certeros cuanto mayor sea la muestra.

No obstante, suponiendo que la muestra sea aleatoria, estamos en condiciones de acotar el error con un cierto grado de confianza, es
decir, de aportar un intervalo en el cual esperamos que se encuentre el valor desconocido del parámetro poblacional.

Intervalo de confianza para la media: el intervalo al 95% de confianza para la media poblacional µ de una variable numérica a partir de una muestra de tamaño n con media 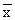y desviación típica s es, según

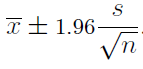
Así pues, el margen máximo de error de la estimación 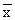con una confianza del 95% es:

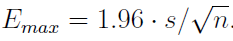
Ejemplo

Se pretende estimar la media,x , de la estatura, que denotamos como X,
de las mujeres de entre 16 y 50 años pertenecientes a una amplia población. Para ello se escogió una muestra (que supondremos aleatoria) de n = 40 mujeres, las cuales aportaron una media aritmética de 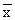= 162.3 cm con una desviación típica de 5.2 cm.

En consecuencia, ya tenemos una estimación puntual de la media x: la media aritmética 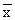= 162.3. El margen máximo de error al 95% de confianza es:

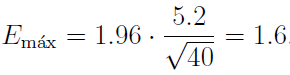
Por lo tanto, el intervalo de confianza al 95% correspondiente es 162.3±1.6. En definitiva, podemos afirmar con una confianza del 95% que la altura media de la población se encuentra entre 160.7 cm y 163.9 cm.