Ejercicio 1
Sea una distribución estadística que viene dada por la siguiente tabla, Noten que la muestra es de n=100:
| xvariable | fabsoluta | FAcumulada |
| 61 | 5 | 5 |
| 64 | 18 | 23 |
| 67 | 42 | 65 |
| 71 | 27 | 92 |
| 73 | 8 | 100 |
Comprobar los siguientes datos:
- La moda, mediana y media.
- El rango, desviación media, varianza y desviación estándar.
Respuestas a comprobar:
- Mo=67
- Me=67
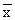 =67.4
=67.4- r=61-73=12
- σ²=6.89785
- σ=2.626
Ejercicio 2
Calcular la media, la mediana y la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
| xvariable | fabsoluta | FAcumulada |
| 2 | 2 | 2 |
| 3 | 2 | 4 |
| 4 | 5 | 9 |
| 5 | 6 | 15 |
| 6 | 2 | 17 |
| 8 | 3 | 20 |
Ejercicio 3
Realizar los cálculos para hallar la varianza y la desviación típica(o estándar) de la siguiente serie de datos: 12, 6, 7, 3, 15, 10, 18, 5.
Ejercicio 4
Hallar la media, mediana y moda de la siguiente serie de números: 3, 5, 2, 6, 5, 9, 5, 2, 8, 6.
Ejercicio 5
Hallar la media, la varianza y la desviación típica de las siguientes 3 series de números:
2, 3, 6, 8, 11.
12, 6, 7, 3, 15, 10, 18, 5.
Ejercicio 6
Dadas las series estadísticas:
- 3, 5, 2, 7, 6, 4, 9
- 3, 5, 2, 7, 6, 4, 9, 1
Calcular:
La moda, la mediana y la media.
La desviación media, la varianza y la desviación típica.
Para el siguiente ejemplo de Desviación Media, las restas quedarán con signo positivo en sus resultados. P ej. 2 – 5.143 quedaría con resultado 3.143 en lugar de -3.143
