Un experimento sigue el modelo de la distribución binomial o de Bernoulli si:
1. En cada prueba del experimento sólo son posibles dos resultados: el suceso A (éxito) y su contrario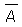
2. La probabilidad del suceso A es constante, es decir, que no varía de una prueba a otra. Se representa por p.
3. El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
La distribución binomial se suele representar por B(n, p).
- n es el número de pruebas de que consta el experimento.
- p es la probabilidad de éxito.
La probabilidad de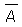 es 1− p, y la representamos por q.
Variable aleatoria binomial
La variable aleatoria binomial, X, expresa el número de éxitos obtenidos en cada prueba del experimento.
La variable binomial es una variable aleatoria discreta, sólo puede tomar los valores 0, 1, 2, 3, 4, …, n suponiendo que se han realizado n pruebas.
La función de probabilidad de la distribución binomial, también denominada función de la distribución de Bernoulli, es:
- n es el número de pruebas.
- k es el número de éxitos.
- p es la probabilidad de éxito.
- q es la probabilidad de fracaso.
El número combinatorio
Ejemplo 1
La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leído. Un grupo de 4 amigos son aficionados a la lectura:
1¿Cuál es la probabilidad de que en el grupo la hayan leído 2 personas?
- n = 4
- p = 0.8
- q = 0.2
- B(4, 0.8)
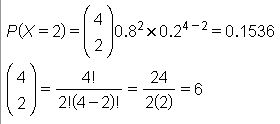
2¿Y cómo máximo 2?
Media
Varianza
Desviación típica
Ejemplo 2
La probabilidad de que un artículo producido por una fabrica sea defectuoso es 0.02. Se envió un cargamento de 10.000 artículos a unos almacenes. Hallar el número esperado de artículos defectuosos, la varianza y la desviación típica.
E