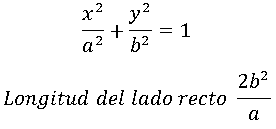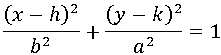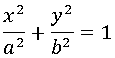Ecuaciones de la Elipse

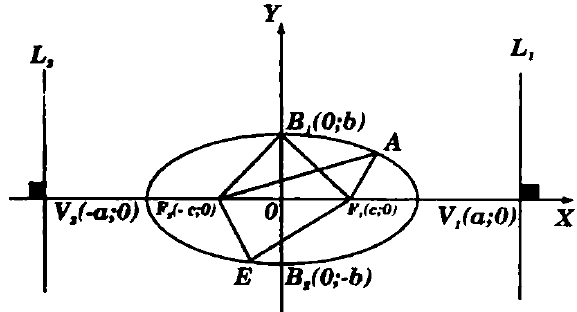
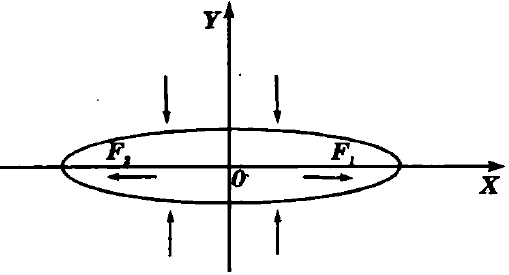
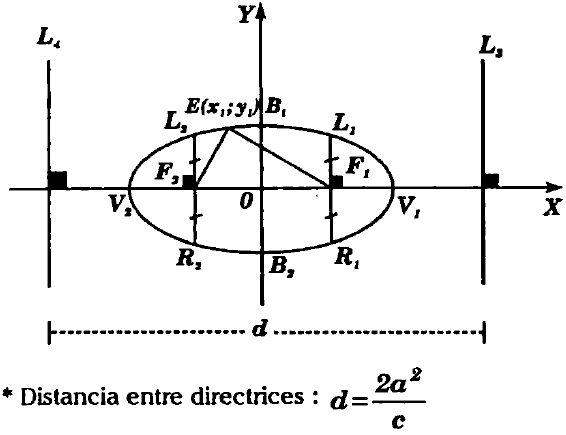
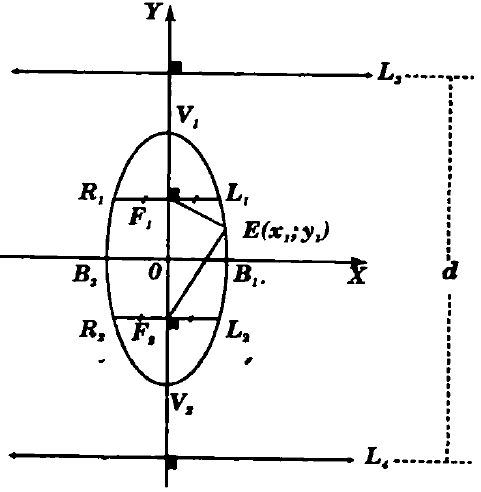
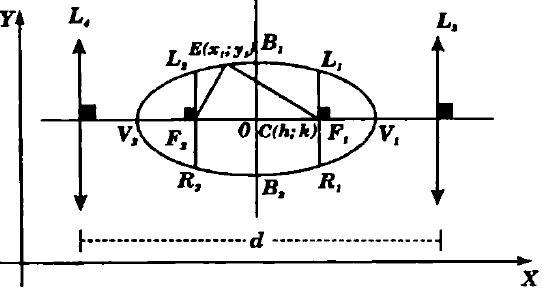
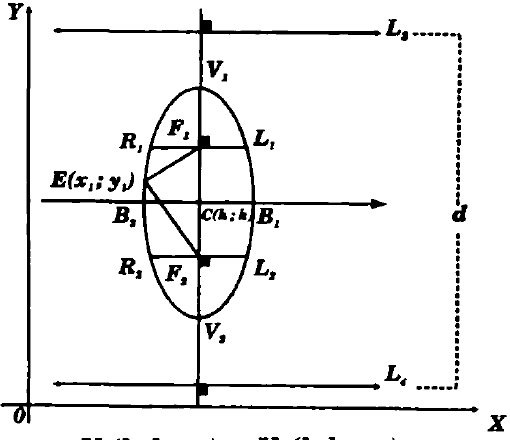
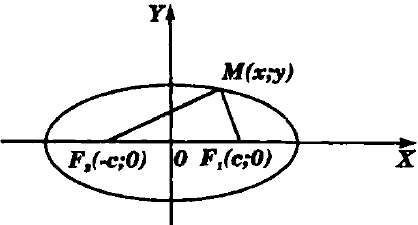
Dados dos puntos fijos F₁ y F₂ distintos, denominados Focos, se define la Elipse como el lugar geométrico del conjunto de puntos P(x;y) tales que la suma de distancias de P a los focos F₁ y F₂, es igual a una constante convencional 2a

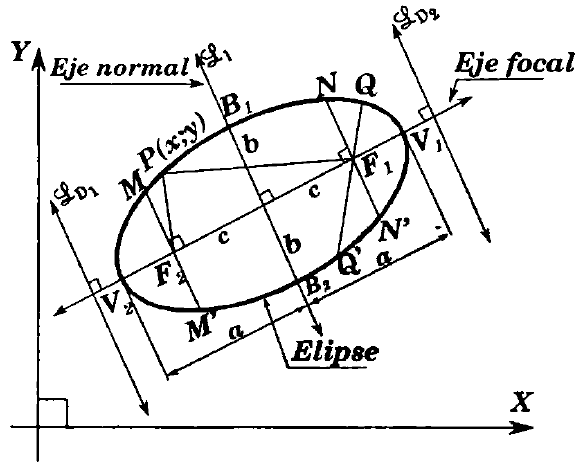
Toda Elipse es simétrica con respecto a sus ejes de simetría, es decir, con respecto al eje mayor y menor.

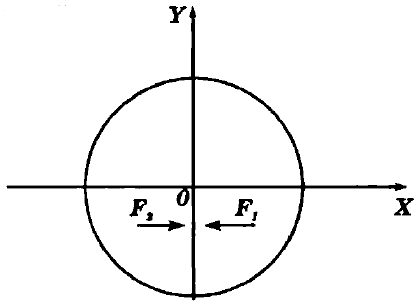
A medida que los focos se acercan y la “e” tiende a 0, la elipse se asemeja mas a una circunferencia:

A medida que los focos se alejan y la “e” tiende a 1, la elipse se asemeja cada vez más a una linea recta

Primera forma(Canónica)

Segunda Forma(Canónica)

Ecuación de una elipse vertical canónica:

Tercera Forma(Ordinaria)

Cuarta Forma(Ordinaria)

Ejemplo 1

Demostrar que la ecuación de una Elipse horizontal canónica es:

Sobre la elipse, tomaremos un punto genérico M(x;y) y luego aplicaremos la definición de la elipse.