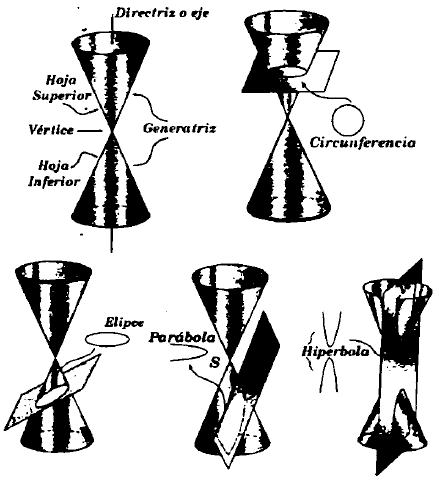
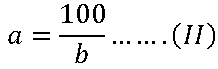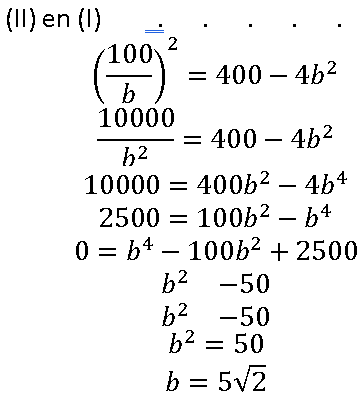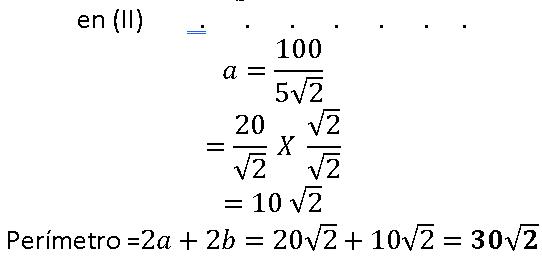Una Sección cónica es la intersección de un plano con un cono

La ecuación general para cualquier sección cónica es:

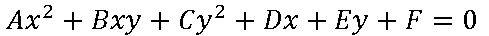
donde A, B, C, D, E y F, son Constantes

• Circunferencia:
  • Si el plano es perpendicular a la Directriz, y no pasa por el vértice, entonces la intersección del plano con el vértice es una Circunferencia.
• Elipse:
  • Si el plano cortante no es paralelo a una Generatriz ni a la Directriz, y no pasa por el vértice del cono, es una Elipse
• Parábola:
  • Cuando el plano cortante es paralelo a una Generatriz y no pasa por el vértice, entonces se forma una Parábola.
• Hipérbola:
  • Si el plano cortante es paralelo a la Directriz del cono y no pasa por el vértice, se genera una Hipérbola

Lugar Geométrico:

Conjunto de puntos que cumplen una misma propiedad. Por ejemplo:

• La Bisectriz de un ángulo.
• La mediatriz de un segmento.
• La circunferencia
• La superficie esférica, etc.

Las cónicas, son denominadas lugares geométricos, porque todos sus puntos cumplen la misma propiedad.

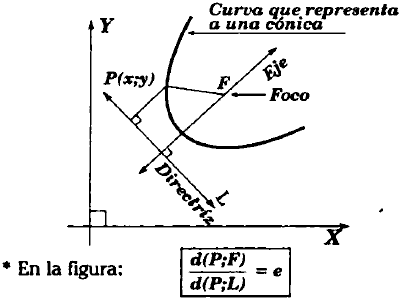
La constante e se denomina excentricidad del lugar geométrico, y determina la forma y tipo de las curvas:

• si e=0, entonces la cónica es una Circunferencia
• si e=1, entonces la cónica es una Parábola
• si e<1, entonces la cónica es una Elipse
• si e>1, entonces la cónica es una Hipérbola

---

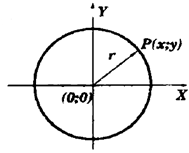
Ecuaciones de la Circunferencia:

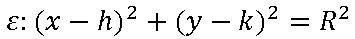
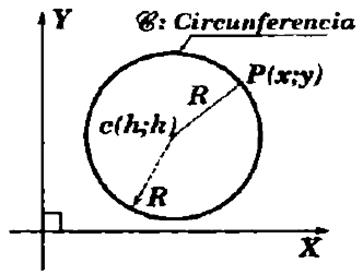
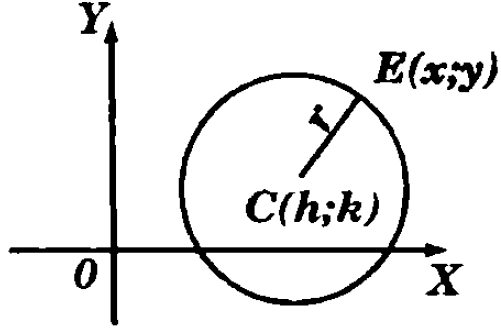
Donde:

• Centro:c(h;k)
• Radio: R
• Punto genérico:P(x;y)

Ecuación Ordinaria de la Circunferencia:

---

---

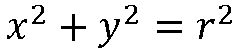
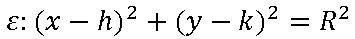
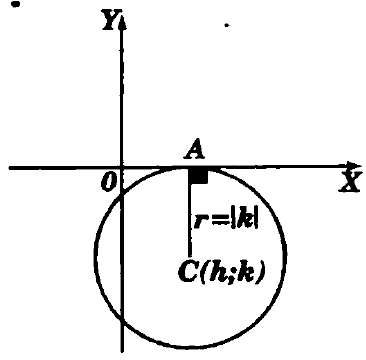
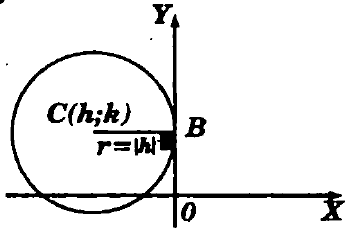
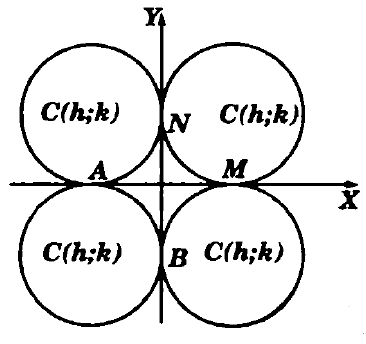
Ecuaciones Particulares de la Circunferencia:

---

Ejemplo:

En la siguiente figura hallar el Perímetro del rectángulo, se sabe que el área del rectángulo es de 100 cm² y que el radio de la circunferencia es 10

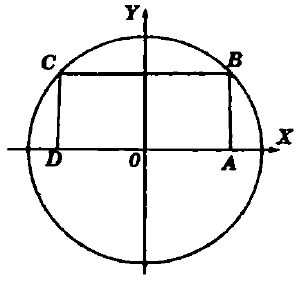
• Perímetro del Rectángulo = ?
• Perímetro del Rectángulo = 2a + 2b = ?
• Ecuación de la Circunferencia: x² + y² = 100 —->a

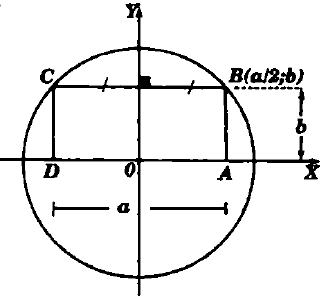
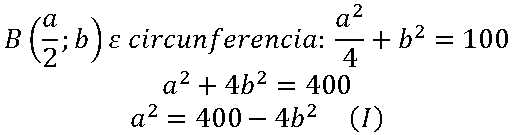
por el dato de que el área del rectángulo=100, se tiene que ab=100