1. Funciones Senoidales

Las funciones senoidales son funciones matemáticas que representan movimientos u oscilaciones periódicas, como las que se encuentran en la corriente alterna (CA) y en las ondas de sonido. La forma general de una función senoidal es:

y(t) = A · sin(ω t + φ)

Donde:

• A: Amplitud, el valor máximo de la onda.
• ω: Frecuencia angular, dada en radianes por segundo.
• t: Tiempo.
• φ: Desfase, que indica un desplazamiento horizontal de la onda respecto al origen.

Los Fasores pueden representarse de 3 formas

2. Equivalencia con Números Complejos

Las funciones senoidales tienen una relación directa con los números complejos a través de la fórmula de Euler, que establece que una función exponencial compleja puede representar tanto el seno como el coseno:

ejθ = cos(θ) + j sin(θ)

Por lo tanto, una señal senoidal puede expresarse en términos de números complejos como:

A · ej(ω t + φ) = A [cos(ω t + φ) + j sin(ω t + φ)]

3. Conversiones de Coordenadas

a. De Polar a Rectangular

En la forma polar, un número complejo se expresa como:

z = r ∠ θ

Donde:

• r: Magnitud del número complejo.
• θ: Ángulo de fase (en radianes o grados).

Para convertir de polar a rectangular, usamos la fórmula:

z = r · [cos(θ) + j sin(θ)]

Las componentes x (parte real) e y (parte imaginaria) del número complejo en forma rectangular son:

x = r · cos(θ)
y = r · sin(θ)

b. De Rectangular a Polar

Para convertir un número complejo de la forma rectangular z = x + jy a su equivalente polar:

La magnitud se calcula como:

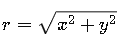
El ángulo se determina como:

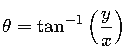
4. Ejemplos Gráficos

Ejemplo 1: Conversión de Polar a Rectangular

Dado z = 5 ∠ 53°

Convertimos a coordenadas rectangulares:

x = 5 · cos(53°) ≈ 5 · 0.6018 = 3.01
y = 5 · sin(53°) ≈ 5 · 0.7986 = 3.99

Entonces, en forma rectangular:

z ≈ 3.01 + j3.99

Ejemplo 2: Conversión de Polar a Rectangular

Función senoidal:

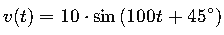
• Magnitud (A): 10
• Ángulo de fase (θ): 45°

Conversión a Fasor: El fasor correspondiente es:

---

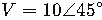
Ejemplo 1: Conversión de Rectangular a Polar

Dado z = 3 + j4

La magnitud es:

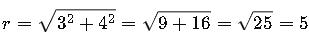
El ángulo es:

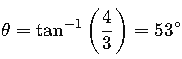
Entonces, en forma polar:

z = 5 ∠ 53° ángulo es:

Ejemplo 2: Conversión de Rectangular a Polar

Operaciones Aritméticas con Números Complejos

Ejercicio 1: Conversión de Función Senoidal a Fasor y de Polar a Rectangular

Ejercicio 2: Operaciones con Números Complejos en Forma Polar y Rectangular