¿Qué es una matriz?
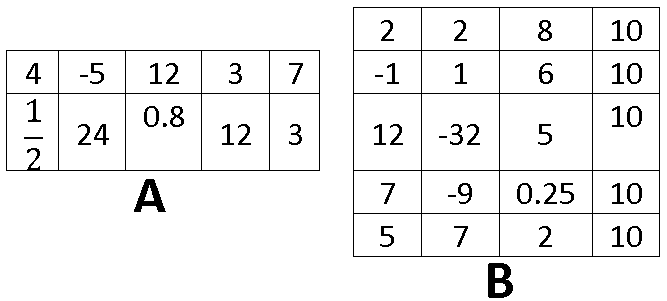
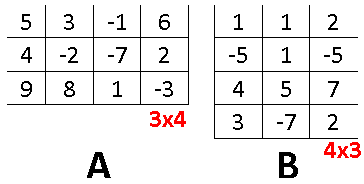
Una matriz es un conjunto de renglones y columnas expresados por un par de números “m x n” denominado orden de la matriz, donde “m” es el número de renglones y “n” el número de columnas.
Operaciones con matrices
Las operaciones básicas que se pueden realizar sobre las matrices son las siguientes:
1. Suma y resta de matrices
2. Multiplicación de una matriz por escalar
3. Multiplicación de matrices
4. Producto cartesiano
Suma de Matrices(A+B)
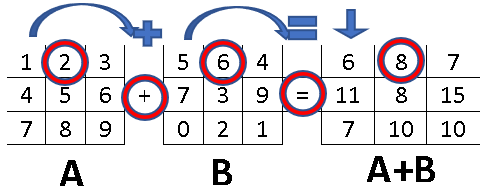
Esta operación se ejecuta al sumar a cada elemento de la matriz “A” con cada elemento de la matriz “B” que se encuentra en la misma posición relativa. La suma se va colocando en la matriz resultante en la misma posición “mn” de los elementos sumados. Ejemplo:
La suma de matrices se da para dos matrices “A” y “B” si son del mismo orden, es decir, de orden “m x n”.
Resta de Matrices (A-B)
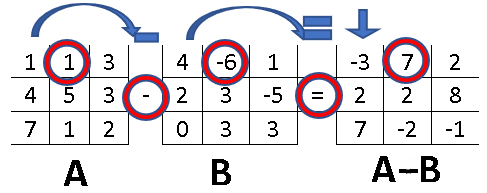
La resta de matrices se denota como “A-B”. La sustracción se lleva a cabo al restar a cada elemento de la matriz “A”, cada elemento de la matriz “B” en la misma posición relativa. La resta se coloca en la matriz resultante en la misma posición mn de los elementos restados.
Como se observa es muy similar a la suma, con la única diferencia del signo de la operación a realizar sobre los elementos de la matriz. Ejemplo:
De igual forma, La resta de matrices se da para dos matrices “A” y “B” del mismo orden, es decir, es de orden “m x n”.
Multiplicación por Escalar
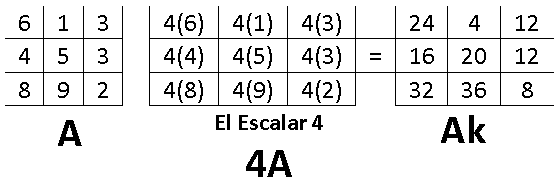
Si se tiene una matriz “A” y un escalar “k”; la multiplicación de una matriz por un escalar se representa con “kA”. Esta operación se realiza al multiplicar cada elemento de la matriz “A” por el escalar “k”, y el resultado se pone en la misma posición relativa en la matriz resultante. Ejemplo:
En esta operación no importa el orden “m x n” de la matriz “A”, es decir, el producto por un escalar está definido para matrices de cualquier orden.
Multiplicación de Matrices
Para esta operación, se tienen dos matrices, “A” y “B”. Para realizar la multiplicación de estas dos, primero se debe establecer la compatibilidad de la operación al revisar que el número de columnas de la matriz “A” sea igual al número de renglones de la matriz “B”.
Por ejemplo, si se tiene una matriz “A” de orden “n x m”, entonces la matriz “B” deberá tener “n” renglones y cualquier número de columnas, por ejemplo, “k”; entonces la matriz resultante será una matriz de orden “n x k”. En estas condiciones operativas, es fácil observar que el proceso de multiplicación de matrices no es conmutativo. Ejemplo:
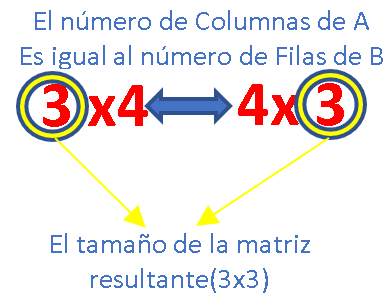
Tenemos entonces que el resultado de esta Multiplicación sería una matriz de 3×3, como se muestra a continuación:
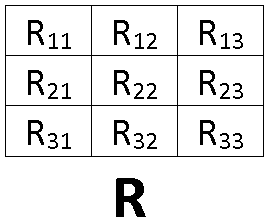
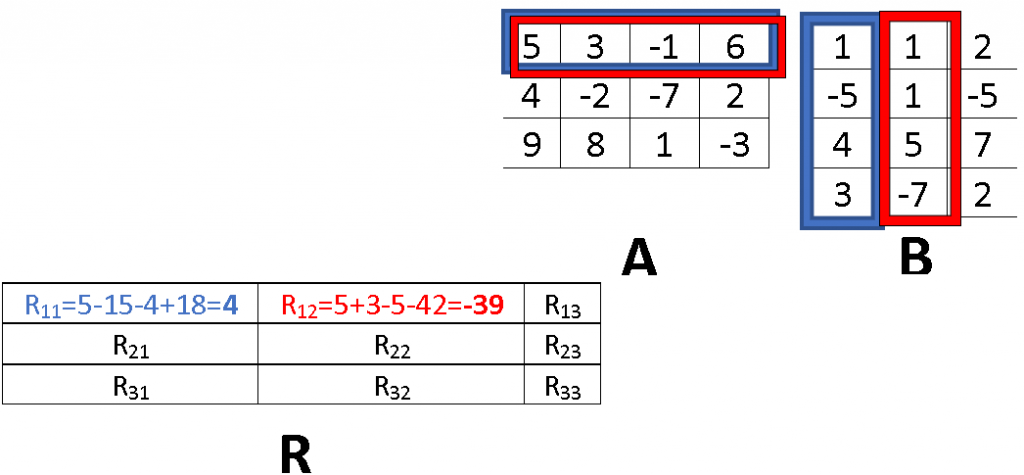
La ubicación de cada elemento de R, nos da la pista de cual Fila multiplicaremos con la Columna correspondiente, en el ejemplo vemos que la fila 1 se multiplica con la Columna 1, luego la Fila 1, con la Columna 2. Los resultados de esas multiplicaciones se van sumando(o restando, dependiendo el signo) y finalmente queda ese valor en la ubicación.
Ejercicios
- Calcular la Suma de A+B de las siguientes matrices:
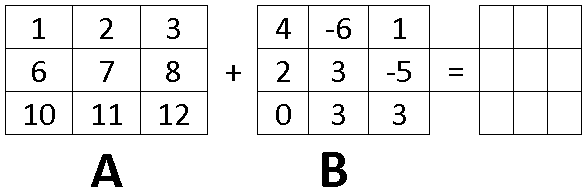
2. Calcular la Resta de A-B de las siguientes matrices:
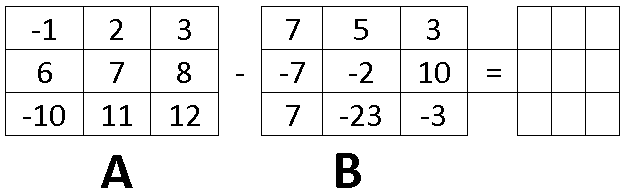
3. Realizar la multiplicación por el escalar (-3) de la siguiente matriz:
4. Calcular la siguiente multiplicación entre matrices: