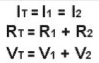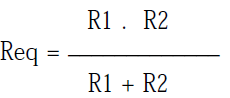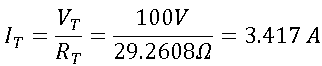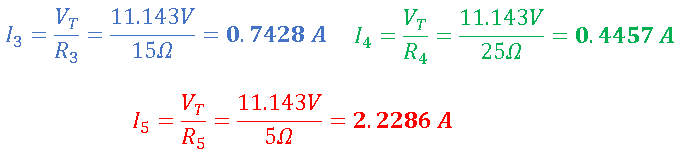A fin de simplificar los circuitos electrónicos es necesario conocer las características de las diferentes combinaciones de resistores/resistencias para establecer componentes equivalentes.

Circuitos en Serie

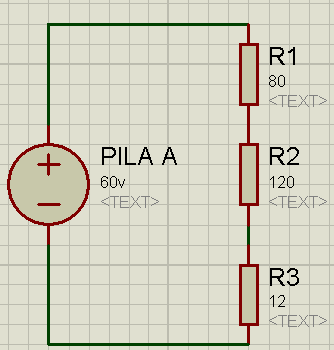
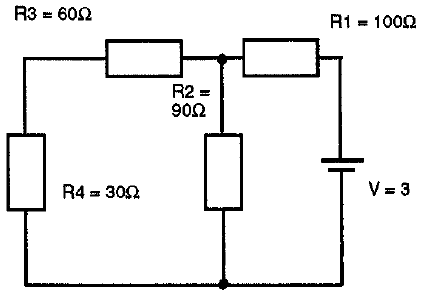
Se dice que dos o más resistores están en serie cuando por ellos circula la misma corriente, de manera que no debe haber ninguna derivación en el camino que origine un cambio en la intensidad de la corriente que circula por ellos.

En la figura anterior, las resistecias R1, R2 y R3 están en serie. La Resistencia equivalente: es una resistencia que puede reemplazar a las del circuito, sin que se modifiquen los parámetros del mismo.

Para calcular la resistencia equivalente de dos o más resistores en serie, simplemente se suman sus valores. En el caso anterior, la resistencia equivalente es: R_eq=R1+R2+R3 o R_e=80+120+12, dando R_e=212 Ω.

Resolveremos para el circuito anterior los siguientes incisos:

1. La corriente eléctrica Total.
2. El voltaje en cada resistencia.

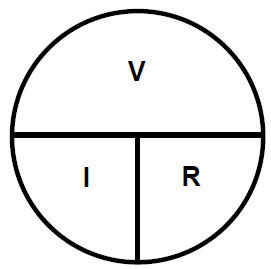
I_T=V_T / R_T

Sabiendo que:

Tenemos:

1). Corriente Total, I_T=V_T / R_T = 60V / 212Ω = 0.2830 Ampers

2). Voltaje en cada resistencia,

V₁=(I₁)(R₁)=(0.2830 A)(80 Ω) = 22.64 V

V₂=(I₂)(R₂)=(0.2830 A)(120 Ω) = 33.96 V

V₃=(I₃)(R₃)=(0.2830 A)(12 Ω) = 3.396 V

V_T = V₁+ V₂ + V₃ = 22.64 + 33.96 + 3.396

V_T = 59.99V ≈ 60V

---

Circuitos en Paralelo

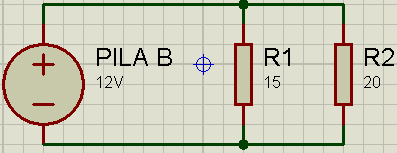
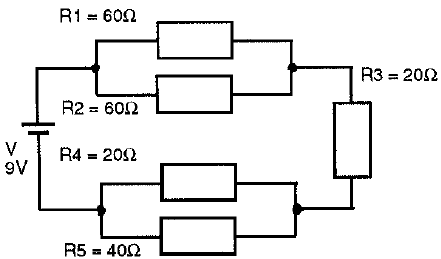
Se dice que dos o más resistores están conectados en paralelo cuando soportan la misma tensión eléctrica(Voltaje), y eso implica que los resistores estén conectados a puntos comunes. Por ejemplo, en la figura anterior, R1 y R2 están en paralelo porque soportan la misma tensión (12V). Para calcular la resistencia equivalente, usamos la siguiente fórmula:

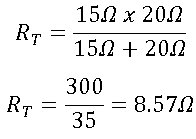
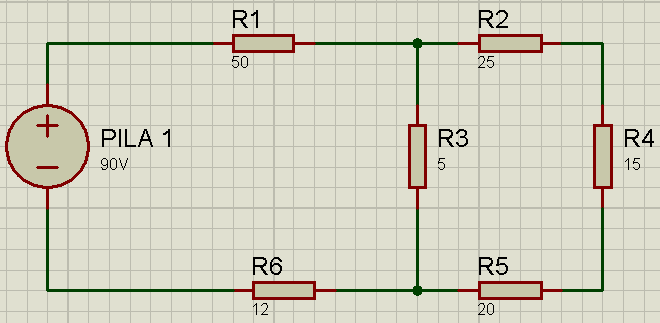
Circuitos Mixtos

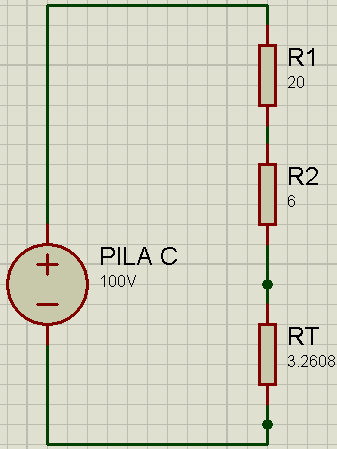
R1 y R2 están en serie, pero no con el resto de las resistencias, pero R3, R4 y R5, están en paralelo, en este caso, no podemos usar la fórmula anterior por estar estar en paralelo estas 3 resistencias.

Resolveremos para el circuito anterior los siguientes incisos:

1. Resistencia Total.
2. Intensidad Total.
3. Voltaje en cada resistencia.
4. Intensidad en cada resistencia

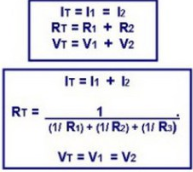
1). Resistencia Total:

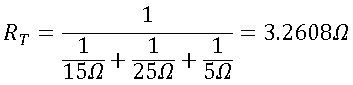
y el circuito quedaría así:

Estando las 3 resistencias en serie, ahora solo las sumamos,

R_T= 20 Ω + 6 Ω + 3.2608 Ω = 29.2608 Ω

¡Es la resistencia en todo el circuito!

2). Intensidad(Corriente) Total,

3). Voltaje en cada resistencia,

V₁=(I₁)(R₁)=(3.417 A)(20 Ω) = 68.34 V

V₂=(I₂)(R₂)=(3.417 A)(6 Ω) = 20.50 V

V₃=(I₃)(R_T)=(3.417 A)(3.2608 Ω) = 11.143 V

V_T = V₁+ V₂ + V₃ = 68.34 + 20.50 + 11.143

V_T = 99.983V ≈ 100V

4). Intensidad en cada resistencia(Notemos que solo se calcula la intensidad de aquellas resistencias que están en paralelo),

---

Importante tener en cuenta otro factor que completa la definición del circuito y los valores de sus resistencias. La Potencia eléctrica consumida en el circuito, que en el caso de las resistencias se transforma íntegramente en calor.

“La potencia disipada en un circuito eléctrico es directamente proporcional al voltaje y la corriente que circula.”

Por lo tanto:

W (watios) = V (voltios) x I (amperios)

Así, por ejemplo, en el circuito más sencillo del primer ejemplo, la potencia de la resistencia deberá ser de al menos:

W = V x I = 12v x 1.4A = 16.8 W

---

Ejercicios

Resolver los siguientes ejercicios:

Ejercicio 1: Determinar,

1. Resistencia Total.
2. Intensidad Total.
3. Voltaje en cada resistencia.
4. Intensidad en cada resistencia

---

Ejercicio 2: Determinar,

1. Resistencia Total.
2. Intensidad Total.
3. Voltaje en cada resistencia.
4. Intensidad en cada resistencia

---

Ejercicio 3: Determinar,

1. Resistencia Total.
2. Intensidad Total.
3. Voltaje en cada resistencia.
4. Intensidad en cada resistencia