Funciones de dos variables
La temperatura T en un punto en la superficie de la Tierra en cualquier momento dado depende de la longitud x y la latitud y del punto. T puede concebirse entonces como una función de dos variables, x y y, o una función del par (x, y). Se indica esta dependencia funcional escribiendo T=f(x, y).

El volumen V de un cilindro circular depende de su radio r y su altura h. De hecho, se sabe que V = πr²h. Se dice que V es una función de r y h y se escribe V(r, h) =πr²h.

Definición

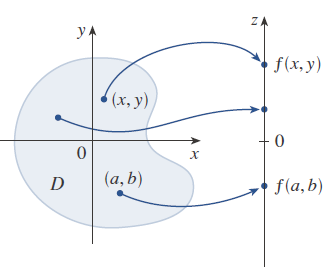
Una función f de dos variables es una regla que asigna a cada par ordenado de números reales (x, y) en un conjunto D un número real único denotado por f (x, y). El conjunto D es el dominio de f y su rango es el conjunto de valores que f adopta, es decir { f(x,y) | (x,y) Є D }

A menudo se escribe z = f(x, y) para explicitar el valor adoptado por f en el punto general (x, f). Las variables x y y son variables independientes y z es la variable dependiente.

---

Ejemplo 1

El índice de viento-frío mide cómo se siente el frío cuando hay viento, basándose en un modelo que calcula la rapidez con que un rostro humano pierde calor. El modelo se desarrolló mediante pruebas clínicas en las que voluntarios se expusieron a varias temperaturas y a velocidades del viento en un túnel aerodinámico refrigerado.

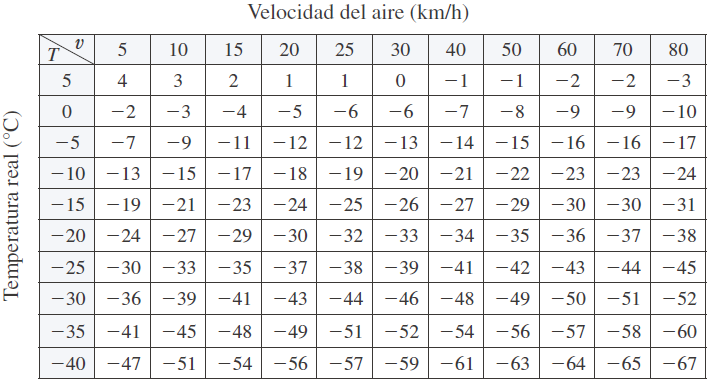
En regiones con clima severo en invierno, el índice de viento-frío suele usarse para describir la aparente severidad del frío. Este índice W es una temperatura subjetiva que depende de la temperatura real T y la velocidad del viento v. Así, W es una función de T y v, y se puede escribir W = f (T, v). La siguiente tabla registra valores de W compilados por el US National Weather Service y el Meteorological Service of Canada.

Índice de viento-frío como función de temperatura del aire y velocidad del viento

La tabla muestra que si la temperatura es de –5 °C y la velocidad del viento de 50 km/h, subjetivamente se sentirá frío y una temperatura cercana a –15 °C. Así,

f( -5, 50 ) = -15

---

Gráficas

Otra manera de visualizar el comportamiento de una función de dos variables es considerar su gráfica.

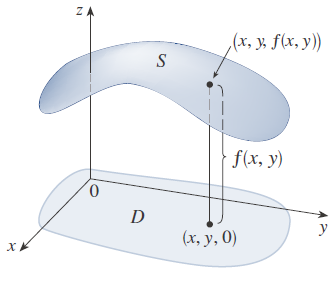
Definición. Si f es una función de dos variables con dominio D, la gráfica de f es el conjunto de todos los puntos (x, y, z) en R³ tales que z=f(x, y) y (x, y) esté en D.

Así como la gráfica de una función f de una variable es una curva C con ecuación y = f(x), la gráfica de una función f de dos variables es una superficie S con ecuación z = f(x, y). Se puede visualizar la gráfica S de f como tendida directamente arriba o abajo de su dominio D en el plano xy, como se muestra a continuación:

Ejemplo 2

Trace la gráfica de la función f (x, y) = 6 – 3x – 2y.

Solución:

La gráfica de f tiene la ecuación z = 6 – 3x – 2y, o 3x + 2y + z = 6, que representa un plano. Para graficar el plano se determinan primero las intersecciones. Si y = z = 0, en la ecuación se obtiene x = 2 como la intersección en x. De igual forma, la intersección en y es 3 y la intersección en z es 6. Esto ayuda a trazar la porción de la gráfica que reside en el primer octante:

La función de este ejemplo anterior es un caso especial de la función.

f( x,y ) = ax + by + c

La cual se llama Función Lineal. La gráfica de esa función tiene la ecuación:

z = ax+ by + c o ax + by – z + c = 0

que es un plano. Así como las funciones lineales de una variable son importantes en el cálculo de una variable, se verá que las funciones lineales de dos variables desempeñan un papel central en el cálculo de múltiples variables.

Ejemplo 3

Trace la gráfica de g(x,y) =

Solución:

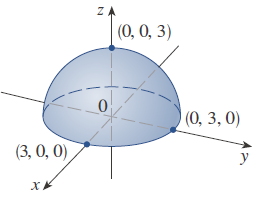
La gráfica tiene la ecuación z = . Eleve al cuadrado ambos miembros de esta ecuación para obtener z² = 9 – x² – y², o x² + y² + z² = 9, la cual se reconoce como una ecuación de la esfera con centro en el origen y radio 3. Pero como z ≥ 0, la gráfica de g es solo la mitad superior de esta esfera:

Nota. Una esfera entera no puede representarse con una sola función de x y y, como se vio en el ejemplo anterior, el hemisferio superior de la esfera x² + y² + z² = 9, es representado por la función

g(x,y)=,

el hemisferio inferior esta representado por

h(x,y)= –

---

Ejemplo 4

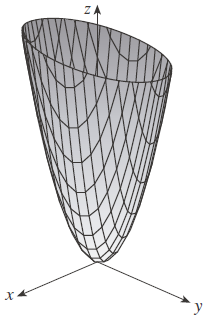
Determine el dominio y el rango y trace la gráfica de h(x,y) = 4x² + y².

Solución:

Nótese que h(x,y) se define para todos los posibles pares ordenados de números reales(x,y), así que el dominio es R², la totalidad del plano xy. El rango de h es el conjunto (0, ∞ ) de todos los números reales no negativos. Nótese también que x²≥ 0 y y²≥ 0, así que h(x,y) ≥ 0 para todas las x y y. La gráfica de h tiene la ecuación z = 4x² + y². Las trazas horizontales son elipses y las verticales parábolas:

---

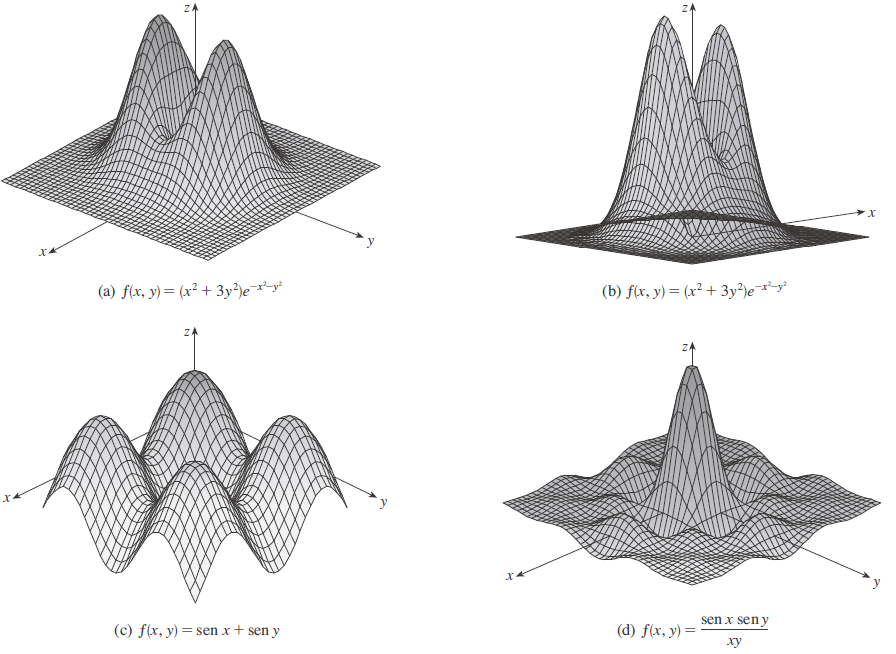
Ejemplo de gráficas generadas por computadora de varias funciones:

Ejercicios:

1. En el ejemplo 1 se consideró la función W = f (T, v), donde W es el índice de viento-frío; T, la temperatura real y v, la velocidad del viento. En la tabla del índice de viento-frio se ofrece una representación numérica.
   1. ¿Cuál es el valor de f(-15,40)?¿Cuál es su significado?
2. El índice I de temperatura-humedad, o humidex, es la temperatura del aire percibida cuando la temperatura real es T y la humedad relativa es h, de modo que se puede escribir I = f (T, h). La tabla de valores de I siguiente es un fragmento de una tabla compilada por Environment Canada. Temperatura aparente como una función de la temperatura y la humedad:
   1. 
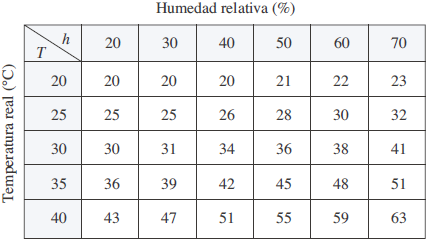
   2. ¿Cuál es el valor de f (35, 60)? ¿Cuál es su significado?
   3. ¿Para qué valor de h es f (30, h) = 36?
   4. ¿Para qué valor de T es f (T, 40) = 42?