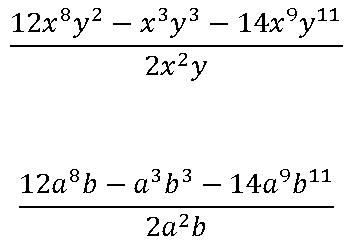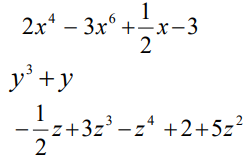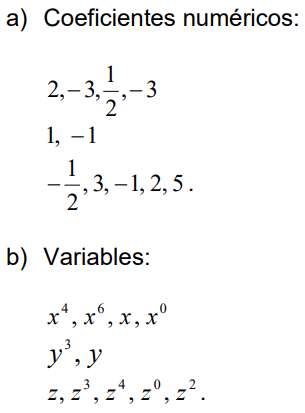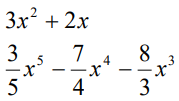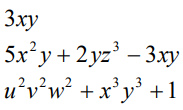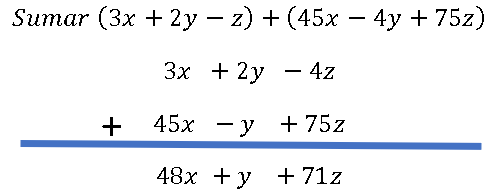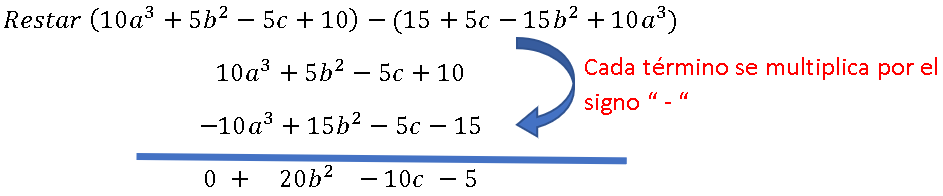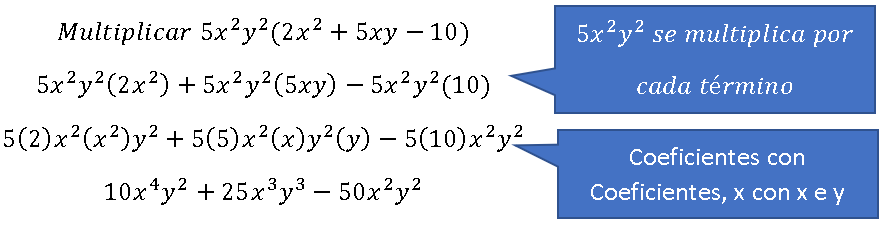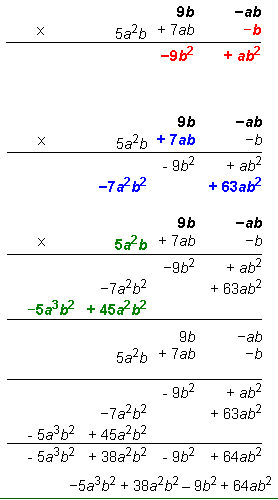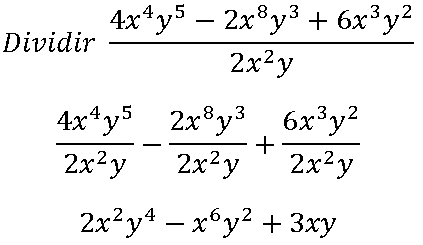Los polinomios se construyen mediante la aplicación repetida de las operaciones elementales de: Potencias, Multiplicaciones, Divisiones, adiciones y restas, P. ej:
A cada expresión se le llama «términos algebraicos» e indican sumas o restas de monomios, las cuales forman Polinomios, van separadas por los signos «+» y «-«, se forman por constantes y variables. Ejemplo:
Las cuales al asociarse se forman los siguientes monomios:
Definición
Un Polinomio es la suma de uno o más términos algebraicos cuyas variables tienen exponentes enteros positivos. Se dividen en Polinomios con Una Variable y Polinomios con Varias Variables.
Clasificación
Un Polinomio con UN Término se llama Monomio, Con DOS Términos se llama Binomio, con TRES Términos es un Trinomio.
Grado
En el Polinomio es la potencia entera positiva mayor de una variable, Ejemplo:
Si los exponentes de una variable disminuyen al ir de izquierda a derecha, se dice que están en orden Descendente, si aumentan de izquierda a derecha, están en orden Ascendente. Ejemplo:
Suma de Polinomios de más de Una Variable
Para sumar polinomios, primero necesitas identificar los términos semejantes en los polinomios y luego combinarlos de acuerdo con operaciones correctas. Como los términos semejantes deben tener exactamente las mismas variables elevadas a la misma potencia, hay que poner atención al identificarlos en los polinomios de múltiples variables.
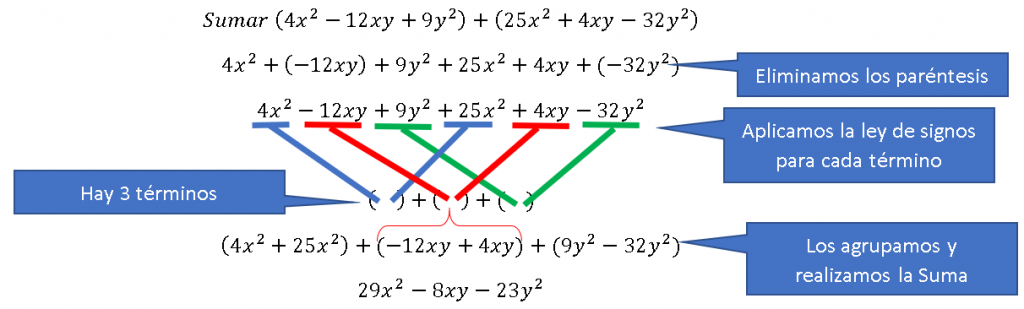
Algunas veces se usan paréntesis para distinguir entre la suma de dos polinomios y la suma de una colección de monomios. En el caso de la suma, puedes simplemente eliminar los paréntesis y realizar la suma.
Ejemplo de SUMA
A algunas personas se les hace más fácil escribir una suma polinomial de manera vertical para combinar los términos semejantes. El proceso de sumar polinomios es el mismo, pero el arreglo de los términos es diferente.
Ejemplo de Suma “vertical”:
Resta de Polinomios de Más de Una Variable
Para restar polinomios con más de una variable, puedes aplicar el mismo proceso usado para restar polinomios con una variable. Para eliminar los paréntesis después del signo de resta, debes multiplicar cada término por −1.
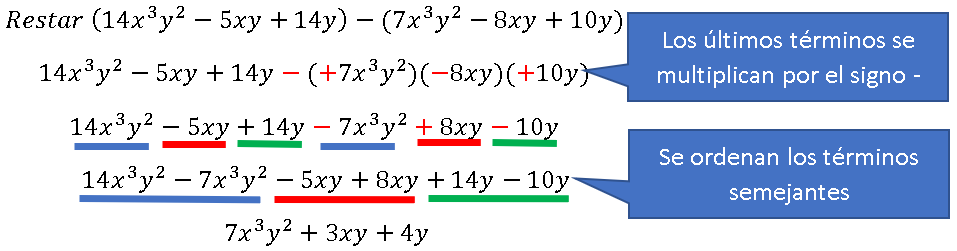
También se puede aplicar el método vertical:
Multiplicación de Polinomios de Más de Una Variable
Usas las mismas técnicas que cuando multiplicas polinomios con una variable. Ejemplo:
(4x2y3)(5x4y2)
Ese es un ejemplo de una multiplicación de dos polinomios, específicamente monomios, con dos variables. Para hacer esta multiplicación, multiplica los coeficientes y usas las reglas de los exponentes para encontrar el exponente para cada variable y calcular el producto. Veamos.
(4x2y3)(5x4y2) = (4 • 5)(x2+4)(y3+2) = 20x6y5
Multiplicar uno monomio por un binomio, usas la propiedad distributiva de la misma forma que cuando multiplicas polinomios de una variable. Ejemplo:
Para multiplicar dos binomios que contienen más de una variable, puedes usar el método FOIL (First, Outer, Inner, Last) que funciona para binomios de una variable. Después de todo, FOIL es simplemente un atajo para usar la propiedad distributiva para multiplicar cada término en un binomio por cada término en el otro binomio. Este proceso funciona para multiplicar cualquier par de binomios. Ejemplo:
El producto de un binomio y un trinomio, cada uno con dos variables, como FOIL sólo puede usarse con el producto de dos binomios, necesitas multiplicar sistemáticamente cada término en el binomio con cada término en el trinomio. Ejemplo:
Al multiplicar polinomios multivariable de esta manera, algunas personas prefieren acomodar la multiplicación de manera vertical. Ejemplo:
División de Polinomios de Más de Una Variable
Los polinomios con más de una variable también pueden dividirse. Cuando divides monomios con más de una variable, divides los coeficientes y luego divides las variables. Cuando hay exponentes con la misma base, las reglas de los exponentes dicen que puedes dividir al restar los exponentes. Ejemplo:
Dividir un trinomio con más de una variable entre un monomio con más de una variable, se sigue el mismo procedimiento que cuando se tiene una variable, pero es necesario poner atención al distinguir entre variables. Ejemplo:
Ejercicios
Sumas:
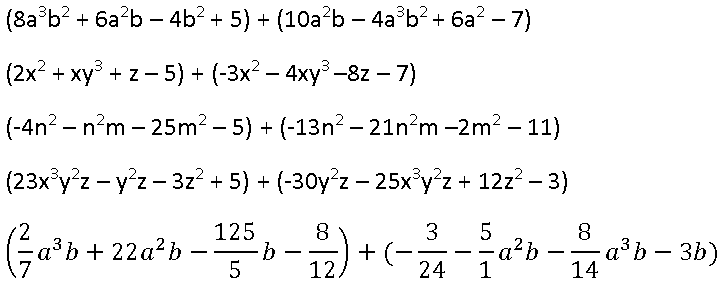
Restas:
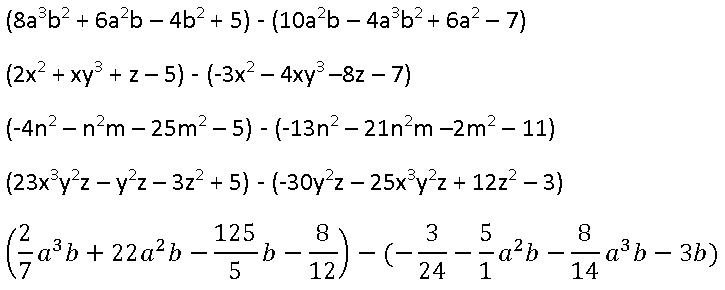
Multiplicaciones
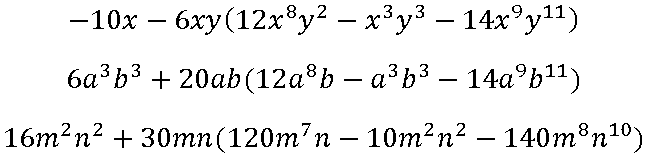
Divisiones