La introducción de las derivadas parciales ocurrió años después del trabajo sobre el cálculo de Newton y Leibniz. Entre 1730 y 1760, Leonhard Euler y Jean Le Rond d’Alembert publicaron por separado varios artículos sobre dinámica en los cuales establecieron gran parte de la teoría de las derivadas parciales. Estos artículos utilizaban funciones de dos o más variables para estudiar problemas de equilibrio, movimiento de fluidos y cuerdas vibrantes.

Por ejemplo, para determinar el efecto de un catalizador en un experimento, un químico podría repetir el experimento varias veces usando cantidades distintas de catalizador, mientras mantiene constantes las otras variables como temperatura y presión. Para determinar la velocidad o la razón de cambio de una función f respecto a una de sus variables independientes se puede utilizar un procedimiento similar. A este proceso se le llama derivación parcial y el resultado se llama derivada parcial de f con respecto a la variable independiente elegida.

Esta definición indica que si z=f(x,y) entonces para hallar f_xse considera y constante y se deriva con respecto a x. De manera similar, para calcular f_y, se considera x constante y se deriva con respecto a y.

Ejemplo 1:

Hallar las derivadas parciales f_x y f_y de la función:

f(x, y) = 3x – x²y² + 2x³y

Si se considera y como constante y se deriva con respecto a x se obtiene:

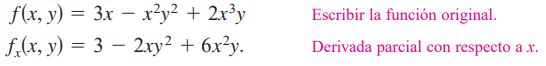
Si se considera x constante y se deriva con respecto a y obtenemos:

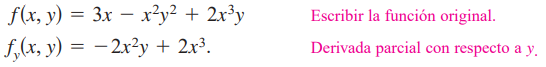
Ejemplo 2, pendientes:

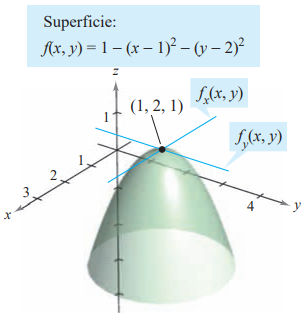
Hallar las pendientes de una superficie en las direcciones de x y de y

Hallar las pendientes de una superficie dadas por:

f(x,y)=1-(x-1)²-(y-2)²

en el punto (1,2,1) en las direcciones de x y y

Ejemplo 3, tasa o razón de cambio:

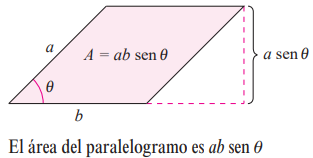
El área de un paralelogramo con lados adyacentes a y b entre los que se forma un ángulo θ está dada por A = ab sen θ.

Ejemplo 4, derivadas de orden superior:

Como sucede con las derivadas ordinarias, es posible hallar las segundas, terceras, etc., derivadas parciales de una función de varias variables, siempre que tales derivadas existan. Las derivadas de orden superior se denotan por el orden al que se hace la derivación. Por ejemplo, la función z=f(x,y) tiene las siguientes derivadas parciales de segundo orden.