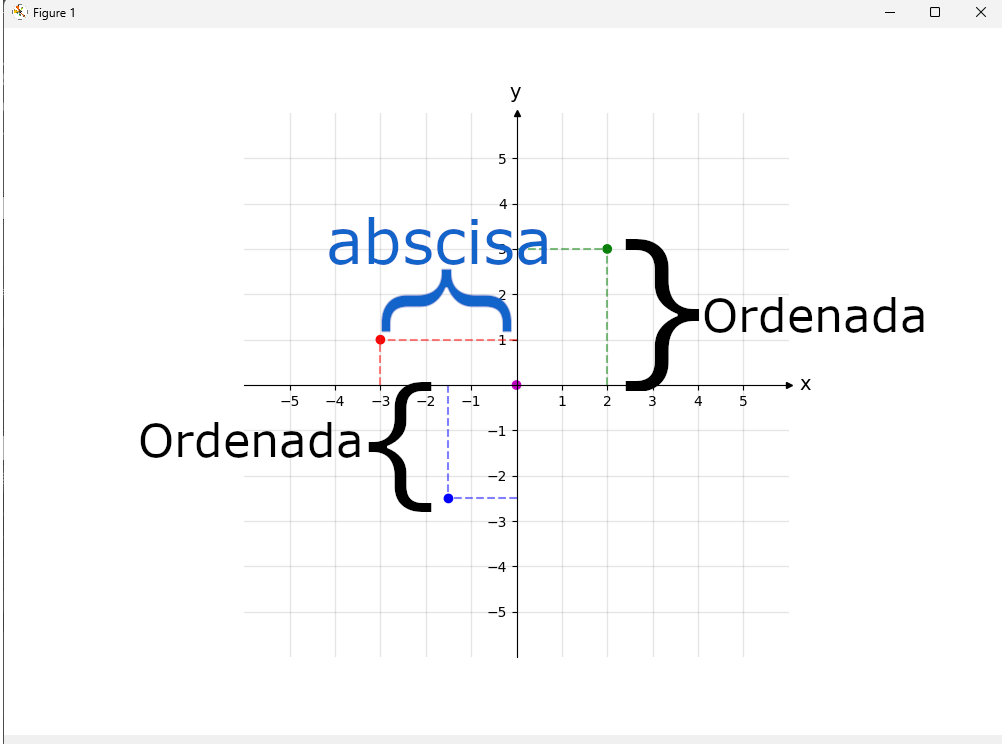
Las dos rectas que dan origen al plano cartesiano deben ser rectas numéricas, pues esa es la condición que hace posible encontrar las ubicaciones de los puntos cualesquiera en el plano. Esta ubicación es la base fundamental de muchos conocimientos comunes en la vida cotidiana, tales como la distancia entre puntos. Una recta numérica es una recta común en el que se estableció una correspondencia con los números reales

El plano cartesiano está formado por dos de estas rectas: Una responsable de la coordenada horizontal y otro responsable de la coordenada vertical. Es común el uso de las letras x para la primera y para la segunda, y los términos «coordenada x» y «coordinada»y».

Fuente: Partes de un plano cartesiano
https://planocartesiano.net/partes-de-un-plano-cartesiano

Cuadrantes

el cruce de las dos rectas rectas numéricas, genera en el plano cartesiano 4 cuadrantes. Existen puntos ubicados a los lados del cero y arriba o abajo, por lo que,

• La región donde “x” y “y” son positivos a la vez, es la llamada del primer cuadrante.
• La región donde “y” es positivo y “x” es negativo es conocida como el segundo cuadrante.
• La región donde “x” e “y” son negativos a la vez, es llamada tercer cuadrante.
• Cuando “x” es positivo y “y” es negativo, los puntos están ubicados en el cuarto cuadrante.

Forma pendiente-intersección( y = mx + b)

Forma ampliamente utilizada para la ecuación de la recta es la forma pendiente-intersección. En esta forma, la ecuación se expresa como y = mx + b, donde m representa la pendiente de la recta y b es el término independiente, es decir, el punto en el eje y donde la recta interseca el plano cartesiano. Esta forma es conveniente cuando se conoce la pendiente y el punto de intersección en el eje y, lo que permite una representación clara y directa de la recta en el plano cartesiano.

La forma general( Ax + By = C)

La forma general de la ecuación de la recta es otra representación importante que se utiliza en diferentes contextos matemáticos. Esta forma se expresa como Ax + By = C, donde A, B, y C son constantes que representan los coeficientes de las variables x e y. Aunque esta forma puede parecer menos intuitiva que las anteriores, es útil para realizar operaciones algebraicas y transformaciones geométricas de la recta.