Perímetro, área y volumen
- Perímetro:
- Definición: Es la distancia total alrededor de una figura geométrica plana.
- Figuras comunes:
- Cuadrado: Todos los lados iguales.
- Rectángulo: Lados opuestos iguales.
- Círculo: Forma redonda, definida por su radio.
- Fórmulas:
- Cuadrado: 𝑃 = 4 × lado
- Rectángulo: 𝑃 = 2 × ( largo + ancho )
- Círculo: 𝑃 = 2 𝜋 𝑟(circunferencia)
- Área:
- Definición: Es la medida de la superficie que ocupa una figura geométrica plana.
- Figuras comunes:
- Cuadrado: Superficie con cuatro lados iguales.
- Rectángulo: Superficie con lados opuestos iguales.
- Círculo: Superficie circular definida por su radio.
- Fórmulas:
- Cuadrado: 𝐴 = lado 2
- Rectángulo: 𝐴 = largo × ancho
- Círculo: 𝐴 = 𝜋 𝑟 2
- Volumen:
- Definición: Es la cantidad de espacio que ocupa un cuerpo geométrico tridimensional.
- Cuerpos geométricos comunes:
- Cubo: Sólido con seis caras cuadradas iguales.
- Prisma rectangular (o paralelepípedo): Sólido con bases rectangulares.
- Esfera: Sólido perfectamente redondo, definido por su radio.
- Cilindro: Sólido con dos bases circulares y una superficie lateral.
- Fórmulas:
- Cubo: V=lado3
- Prisma rectangular: V=largo×ancho×alto
- Esfera: V=4⁄3 𝜋 𝑟 3
- Cilindro: V=𝜋 𝑟 2×altura
Identificación de Figuras y Cuerpos Geométricos
- Figuras planas (2D):
- Triángulo: Tres lados y tres ángulos.
- Cuadrado: Cuatro lados iguales y cuatro ángulos rectos.
- Rectángulo: Cuatro lados, con lados opuestos iguales y cuatro ángulos rectos.
- Círculo: Figura redonda definida por su radio.
- Cuerpos geométricos (3D):
- Cubo: Seis caras cuadradas iguales.
- Prisma rectangular: Seis caras rectangulares, con pares opuestos iguales.
- Esfera: Superficie redonda continua.
- Cilindro: Dos bases circulares y una superficie lateral curva.
Elementos de Figuras y Cuerpos Geométricos
- Lado: Segmento que forma parte del perímetro de una figura plana.
- Radio: Distancia del centro a cualquier punto de la circunferencia (círculo o esfera).
- Altura: Distancia entre las bases en prismas y cilindros.
- Base: La cara inferior de un sólido o una de las caras en prismas y cilindros.
- Cara: Cada una de las superficies planas de un cuerpo geométrico.
- Aristas: Bordes de las caras.
- Vértices: Punto donde concurren las aristas.
- Ángulos planos: Formados por dos aristas.
- Ángulos diédricos: Formados por dos caras.
- Ángulos poliédricos: Formados por 3 o más caras o vértices.
- Diagonales: Que unen dos vértices no consecutivos de una misma cara.
- Radio: Distancia del centro a cualquier punto de la circunferencia
Estos conceptos y fórmulas son fundamentales en geometría y permiten calcular propiedades esenciales de las figuras y cuerpos geométricos.
Conceptos Básicos sobre Ángulos y Triángulos
Ángulos
- Definición de Ángulo:
- Es la abertura formada por dos rayos que tienen un extremo común llamado vértice.
- Tipos de Ángulos:
- Ángulo agudo: Menor de 90 grados.
- Ángulo recto: Exactamente 90 grados.
- Ángulo obtuso: Mayor de 90 grados pero menor de 180 grados.
- Ángulo llano: Exactamente 180 grados.
- Ángulo completo: Exactamente 360 grados.
- Elementos de un Ángulo:
- Vértice: Punto donde se encuentran los dos rayos.
- Lados: Los dos rayos que forman el ángulo.
- Medición de Ángulos:
- Se mide en grados (°), minutos (‘) y segundos («).
Ángulos y sus unidades de medida: grados sexagesimales y radianes
Grados Sexagesimales (°):
- El sistema sexagesimal divide el círculo en 360 partes iguales, cada una de las cuales es un grado.
- Cada grado se divide en 60 minutos (‘) y cada minuto en 60 segundos («).
- Ejemplo: 1 grado = 60 minutos = 3600 segundos.
Radianes (rad):
- Un radián es la medida del ángulo subtendido por un arco de un círculo cuya longitud es igual al radio del círculo.
- En un círculo completo, hay 2π radianes.
- Ejemplo: Un círculo completo (360°) es igual a 2π radianes.
Ejemplo 1: Medición de un Ángulo en Navegación
Un marinero necesita ajustar el rumbo de su barco para llegar a un destino específico. Al usar su brújula, determina que debe girar 125 grados, 30 minutos, y 15 segundos hacia el este.
- Ángulo en grados, minutos y segundos: 125° 30′ 15″
- Interpretación:
- El ángulo de giro total es 125 grados.
- Además, se suman 30 minutos, que son la mitad de un grado.
- Finalmente, se agregan 15 segundos, que son una fracción muy pequeña de un grado (1/240 de un grado).
Ejemplo 2: Astronomía y Medición de Estrellas
Un astrónomo está observando una estrella y quiere registrar su posición exacta en el cielo. Utiliza un telescopio con un círculo graduado y determina que la posición de la estrella es 45 grados, 20 minutos y 50 segundos desde el horizonte.
- Ángulo en grados, minutos y segundos: 45° 20′ 50″
- Interpretación:
- El ángulo de elevación de la estrella es 45 grados.
- Además, se suman 20 minutos, que son un tercio de un grado.
- Finalmente, se agregan 50 segundos, que es poco menos de un minuto (50/60 de un minuto).
Conversión de estos valores a una sola unidad (opcional)
Ejemplo 1:
Convertir 125° 30′ 15″ a grados decimales:
125° + ( 30′ ⁄ 60) + ( 15» ⁄ 3600)
125° + 0.5° + 0.0041667° ≈ 125.504167°
Ejemplo 2:
Convertir 45° 20′ 50″ a grados decimales:
45° + ( 20′ ⁄ 60) + ( 50» ⁄ 3600)
45° + 0.333333° + 0.0138889° ≈ 45.347222°
Estos ejemplos ilustran cómo se usan los grados, minutos y segundos en el sistema sexagesimal para medir ángulos con precisión en diferentes contextos prácticos.
Triángulos
- Definición de Triángulo:
- Es una figura geométrica plana formada por tres lados y tres ángulos.
- Clasificación de Triángulos según sus Lados:
- Triángulo equilátero: Tres lados iguales.
- Triángulo isósceles: Dos lados iguales.
- Triángulo escaleno: Ningún lado igual.
- Clasificación de Triángulos según sus Ángulos:
- Triángulo acutángulo: Tres ángulos agudos.
- Triángulo rectángulo: Un ángulo recto.
- Triángulo obtusángulo: Un ángulo obtuso.
- Elementos de un Triángulo:
- Lados: Segmentos que forman el triángulo.
- Vértices: Puntos donde se unen los lados.
- Ángulos internos: Ángulos formados entre dos lados del triángulo.
- Ángulos externos: Ángulos formados por un lado del triángulo y la prolongación de otro lado.
- Propiedades de los Triángulos:
- Suma de ángulos internos: La suma de los ángulos internos de un triángulo es siempre 180 grados.
- Inecuación triangular: La suma de las longitudes de dos lados de un triángulo siempre es mayor que la longitud del tercer lado.
- Teoremas y Fórmulas Relacionadas:
- Teorema de Pitágoras (para triángulos rectángulos): a2+b2=c2, donde c es la hipotenusa.
- Área de un Triángulo:
- General: A=1⁄2 ×base×altura
- Ley de los Senos
- Ley de los Cosenos
Ejemplos:
Ejemplo 1
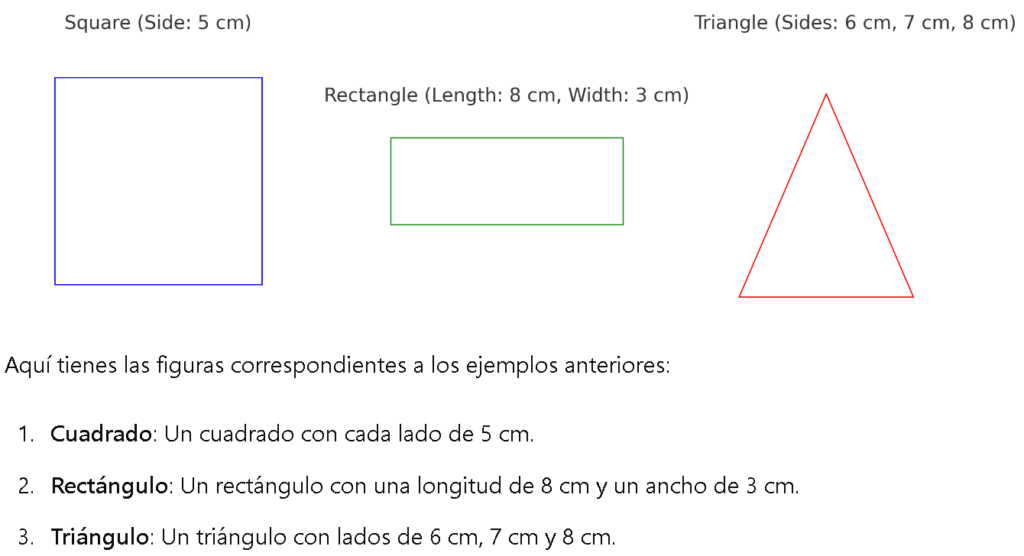
Perímetro de un Cuadrado Problema: Calcular el perímetro de un cuadrado cuya longitud de lado es 5 cm.
Solución: El perímetro de un cuadrado se calcula sumando las longitudes de sus cuatro lados. Como todos los lados de un cuadrado son iguales, la fórmula es:
𝑃 = 4 × lado
P=4×5cm
𝑃 = 20 cm; Respuesta: El perímetro del cuadrado es 20 cm.
Ejemplo 2
Perímetro de un Rectángulo Problema: Calcular el perímetro de un rectángulo con una longitud de 8 cm y un ancho de 3 cm.
Solución: El perímetro de un rectángulo se calcula sumando las longitudes de sus cuatro lados. La fórmula es:
𝑃 = 2 × ( largo + ancho )
𝑃 = 2 × ( 8 cm + 3 cm )
𝑃 = 2 × 11 cm
𝑃 = 22 cm; Respuesta: El perímetro del rectángulo es 22 cm.
Ejemplo 3
Perímetro de un Triángulo Problema: Calcular el perímetro de un triángulo cuyos lados miden 6 cm, 7 cm y 8 cm. Solución: El perímetro de un triángulo se calcula sumando las longitudes de sus tres lados. La fórmula es:
𝑃 = lado 1 + lado 2 + lado 3
𝑃 = 6 cm + 7 cm + 8 cm
𝑃 = 21 cm; Respuesta: El perímetro del triángulo es 21 cm
Área y Perímetro: Un terreno tiene la siguiente forma:
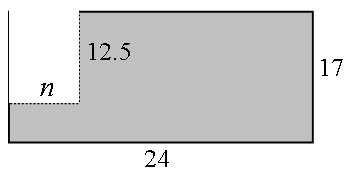
- ¿Cuál es la expresión algebraica que representa el área del terreno? A=24 x 17 – (12.5 x n)
- Si el valor de n es 6 metros, ¿cuántos metros cuadrados tiene el terreno? A=333m2
- ¿Cuál es el perímetro del terreno?P=82m
Ejercicios:
Ejercicio 1:
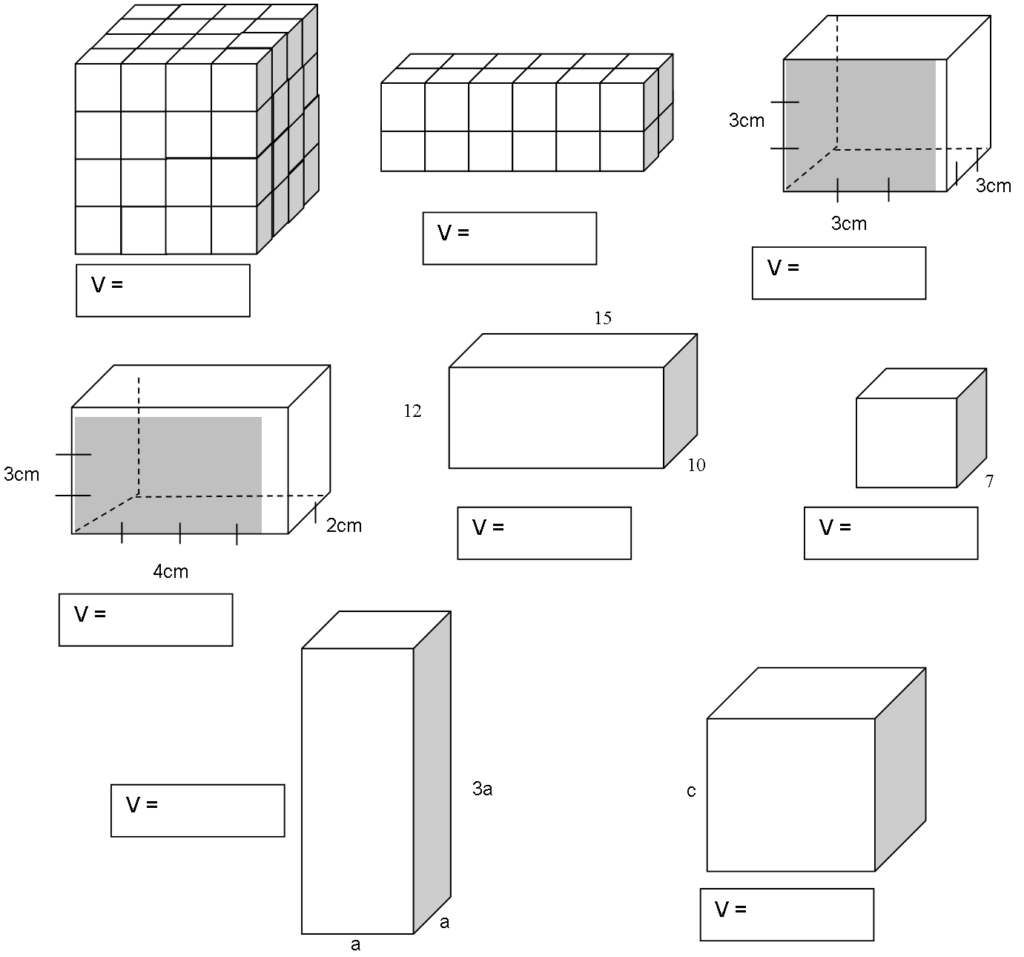
Ejercicio 2:
Calcula el perímetro de la siguiente figura, sabiendo que x = 3 cm y y = 1.5 cm: