En física existen muchas magnitudes que poseen módulo y dirección, y se suman como los desplazamientos. Son ejemplos la velocidad, la aceleración, el momento lineal y la fuerza. Estas magnitudes se llaman vectores. Las magnitudes que carecen de dirección asociada –por ejemplo, la distancia y el módulo de la velocidad— se denominan escalares.
Un vector es representado por una Flecha
Vector X Escalar
Un vector A multiplicado por un escalar s es el vector B = sA, que tiene módulo |s| A y es paralelo a A si s es positivo, y antiparalelo a A si s es negativo. Así, el vector -A tiene el mismo módulo que A, pero apunta en dirección opuesta, de modo que A + (—A) = O. Las dimensiones de sA son las de s multiplicadas por las de A.
Resta de Vectores
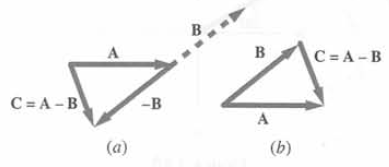
Para restar el vector B del vector A basta sumarle —B. El resultado es C = A + (—B) = A — B(fig. a). Otro método equivalente de restar B de A es unir sus orígenes y trazar el vector C de B a A. Es decir, C es el vector que debe sumarse a B para obtener el vector resultante A (fig. b). Las reglas de sumar o restar dos vectores cualesquiera, tales como dos vectores velocidad o dos vectores aceleración, son las mismas que las utilizadas para los desplazamientos.
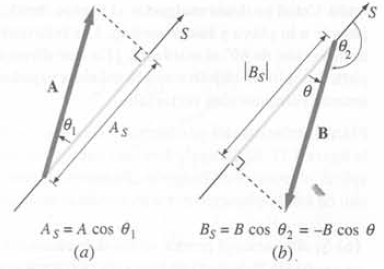
La componente de un vector a lo largo de una línea en el espacio es la longitud de la proyección del vector sobre dicha línea. Se obtiene trazando una línea perpendicular desde el extremo o flecha de un vector a la línea, como indica la siguiente figura.
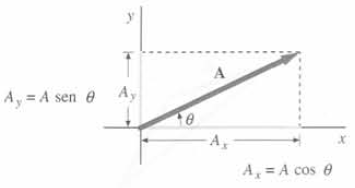
Las componentes de un vector a lo largo de las direcciones x, y y z, ilus-tradas en la siguiente figura para un vector en el plano xy, se denominan componentes rectangulares.
Ejemplo:
Suponga que usted trabaja como animador en un centro turístico en una isla tropical. Dispone de un mapa que le indica las direcciones a seguir para enterrar un tesoro en un lugar determinado. Usted no desea malgastar el tiempo dando vueltas por la isla, porque quiere acabar pronto para ir a la playa y hacer surfing. Las instrucciones son ir 3 km hacia el oeste y luego 4 km en la dirección de 60″ al noroeste. ¿En qué dirección debe moverse y cuánto tendrá que caminar para cumplir su objetivo con la máxima rapidez? Encuentre la respuesta (a) gráficamente y (b) usando componentes vectoriales.
Planteamiento del problema: Hay que encontrar la resultante del desplazamiento. que es C en la figura a continuación. El triángulo formado por los tres vectores no es rectangular. de modo que no podemos aplicar el teorema de Pitágoras. Podemos obtener gráficamente la resultante dibujando a escala cada uno de los desplazamientos y midiendo el desplazamiento resultante.
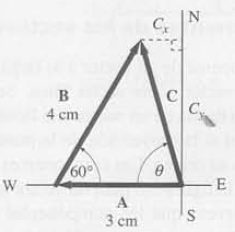
a). Si dibujamos el primer vector desplazamiento A de 3 cm de largo y el segundo 13 de 4 cm de largo. encontraremos que el vector resultante C es de unos 3,5 cm de longitud. Así, el módulo del desplazamiento resultante es de 15 km. El ángulo Ø formado por el desplazamiento resultante y la dirección oeste puede medirse con un transportador angular. Por lo tanto, debe andar 3.5 km a 75′.