Teorema de Pitágoras
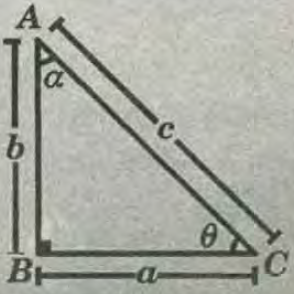
Es una proposición atribuida a Pitágoras en la que en todo Triángulo Rectángulo, El cuadrado de la Longitud de su Hipotenusa es igual a la Suma de los cuadrados de las Longitudes de los Catetos.
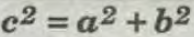
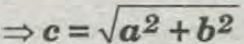
Sobre Perímetro, Área y Volumen
1. El perímetro de un polígono (o cualquier otra curva cerrada, tal como un círculo) es la distancia alrededor del exterior.
2. El área de una curva simple, cerrada o plana es la cantidad del espacio interior.
3. El volumen de un solido de forma 3D es la cantidad del espacio desplazado por el.
Algunas fórmulas para figuras planas comunes de 2 dimensiones y sólidos de 3 dimensiones se dan a continuación. Las respuestas tienen una, dos, o tres dimensiones; el perímetro es medido en unidades lineales , el área es medido en unidades cuadradas , y el volumen es medido en unidades cúbicas
(más…)Ecuaciones Diferenciales
Si se quiere determinar la posición de una partícula móvil conociendo su velocidad o aceleración; o bien, dada una sustancia radiactiva que se desintegra, con coeficiente de variación conocido, se trata de determinar la cantidad de sustancia remanente después de un tiempo dado. Vemos que en ejemplos como éstos, se trata de determinar una función desconocida mediante datos relacionados por una ecuación que contiene por lo menos una de las derivadas de la función desconocida. Estas ecuaciones se denominan Ecuaciones Diferenciales y su estudio constituye una de las ramas de la Matemática que tienen más aplicaciones.
Resumiendo podríamos decir que son Ecuaciones con términos donde figuran Derivadas o Diferenciales, las podemos ordenar por Tipo, Orden y Linealidad.
(más…)Ecuación lineal con una incógnita
Igualdad, expresión de que dos cantidades o expresiones algebraicas tienen el mismo Valor.
Ecuación, igualdad donde hay cantidades desconocidas llamadas incógnitas, quienes son representadas por las últimas letras del alfabeto: x, y, z, u, v, Ejemplo:
5x + 2 =17
(más…)Productos notables
Se le llama Productos notables a aquellas multiplicaciones que cumplen reglas fijas y cuyo resultado puede ser dado por simple inspección, es decir, sin verificación.

Ejercicios de las operaciones fundamentales
Ejercicios de cantidades positivas y negativas
- Pedro debía 60 pesos, y recibió 320. Expresar su estado económico.
- Un hombre que tenla 1170 pesos, hizo una compra por valor de 1510. Expresar su estado económica.
- Tenía $200. Cobré $50 y pagué deudas por $189.¿Cuánto tengo?
- Compro ropa por valor de 665 pesos y alimentos por 1178. Si tenía 2280, ¿cuánto es lo que me queda?.
- Tenía $20. Pague $15 que debía, después cobré $40 y luego hice gastos por $75. ¿cuánto tengo?
- A las 9 a.m. el termómetro marca +12º y de ésta hora a las 8 p.m. ha bajado 15°. Expresar la temperatura a las 8 p.m.
- A las 6 a.m. el termómetro marca -3°. A las 10 a.m. la temperatura es 8° más alta y desde esta hora hasta las 9 p.m. ha bajado 6°. Expresar la temperatura a las 9 p.m.
- A la 1 p.m. el termómetro marca +15º y a las 10 p.m. marca -3°. ¿Cuántos grados ha bajado la temperatura?
- A las 3 a.m. el termómetro marca -8° y al mediodía +5°. ¿Cuántos grados ha subido la temperatura?
- A las 8 a.m. el termómetro marca -4°; a las 9 a.m. ha subido 7° ; a las 4 p.m. ha subido 2° más y a las 11 p.m. ha bajado 11°. Expresar la temperatura a las 11 p.m.
Herramientas Informáticas
Sistemas Operativos
(más…)Un sistema operativo es el software principal o conjunto de programas de un sistema informático que gestiona los recursos de hardware y provee servicios a los programas de aplicación de software
Generalidades de la Calidad
Definiciones de calidad del software.
“Concordancia con los requisitos funcionales y de rendimiento explícitamente establecidos con los estándares de desarrollo explícitamente documentados y con las características implícitas que se espera de todo software desarrollado profesionalmente” R. S. Pressman (1992).
“El conjunto de características de una entidad que le confieren su aptitud para satisfacer las necesidades expresadas y las implícitas” ISO 8402 (UNE 66-001-92).

2. Prueba de Hipótesis Estadística
H0, Hn, Errores Tipo I y II
La prueba de hipótesis estadística es otra forma de inferencia que se utiliza para aceptar o rechazar hipótesis sobre un fenómeno aleatorio;no se puede considerar como una prueba definitiva, ya que en ella se establece un criterio o regla de decisión para aceptar o rechazar una hipótesis y, la regla de decisión está asociada con ciertos riesgos.
Procedimiento General
(más…)