Conjunto de los Números Reales

Descripción:

El conjunto de los números reales (R) incluye todos los números que se pueden representar en una recta numérica. Está compuesto por diferentes subconjuntos:

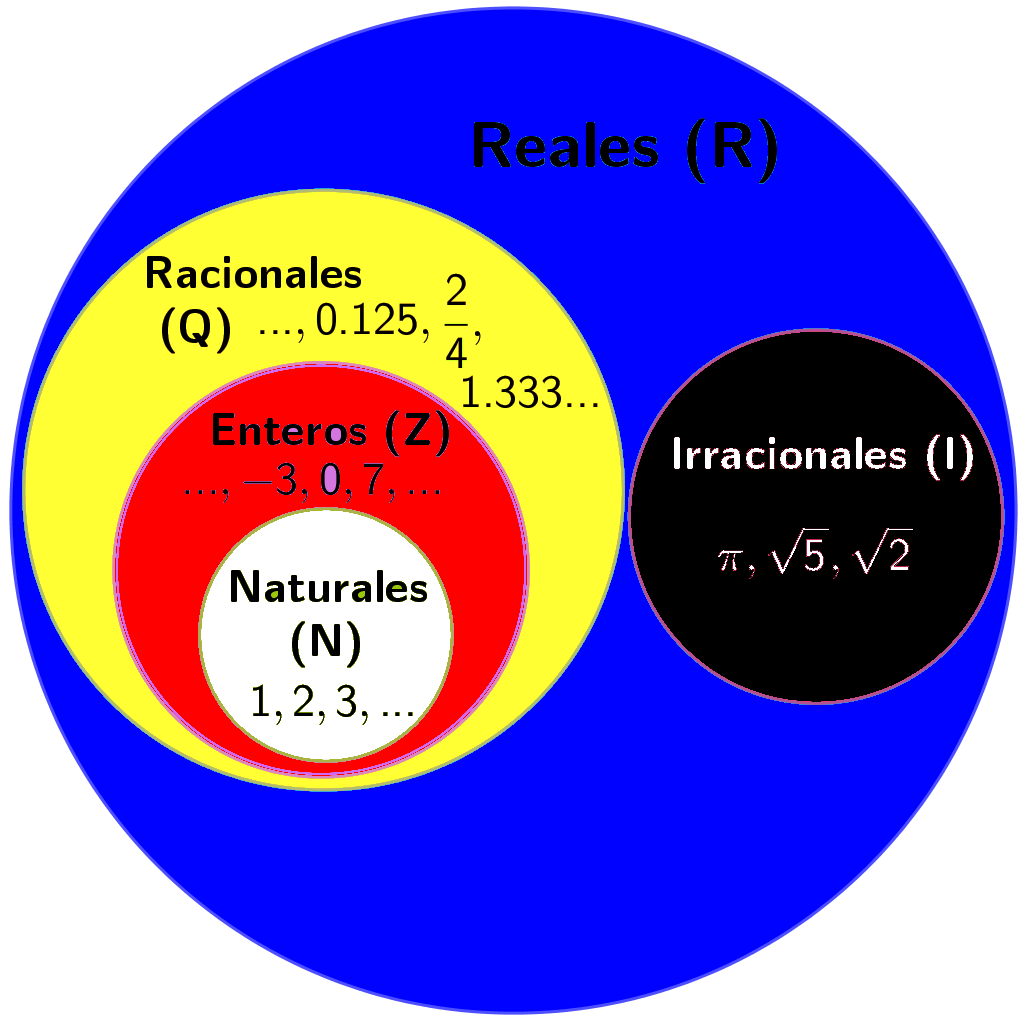
1. Los Numeros Naturales(N) son los enteros que representan existencias de lo que vemos, como 5 dedos, 2 ojos, 108 pétalos, etc, son números enteros positivos, pues en la naturaleza no hay fracciones ni negativos.
2. Los números enteros(Z), son los naturales y sus opuestos(los negativos) así como el cero(0).
3. en Los Números Racionales(Q), encontramos las fracciones, ya sean decimales o fraccionarias, positivas y negativas.
4. Los Números Irracionales(I) son aquellos que no representan una cantidad exacta, como se ejemplifica en la figura anterior.
5. Los Racionales(R) incluye a todos los anteriores

---

1. Variable

• Definición: Es un símbolo que representa un valor que puede cambiar dentro de un contexto matemático o científico.
• Ejemplo 1: En la ecuación y=2x+5y = 2x + 5y=2x+5, x es una variable que puede tomar diferentes valores.
• Ejemplo 2: En un experimento, la temperatura ambiente es una variable que puede cambiar con el tiempo.

2. Variable Dependiente e Independiente

• Variable Independiente: Es aquella cuyo valor no depende de otra variable, sino que se controla o manipula directamente.
• Variable Dependiente: Es aquella que depende del valor de la variable independiente; representa el resultado o efecto.
• Ejemplo 1: En la función y=3x+2:
  • x: Variable independiente (se elige su valor).
  • y: Variable dependiente (su valor depende de x).
• Ejemplo 2: En un experimento sobre el crecimiento de plantas:
  • Variable independiente: Cantidad de agua suministrada.
  • Variable dependiente: Altura de la planta.

3. Constante

• Definición: Es un valor fijo que no cambia dentro de una ecuación o experimento.
• Ejemplo 1: En y=5x+3, el número 3 es una constante.
• Ejemplo 2: La gravedad terrestre g=9.8 m/s² es una constante.

4. Función

• Definición: Es una relación matemática que asigna un valor único de salida (variable dependiente) a cada valor de entrada (variable independiente).
• Ejemplo 1: f(x)=x²(Asigna el cuadrado de x a cada valor de entrada).
• Ejemplo 2: f(x)=2x+1(Relaciona x con un valor aumentado en 1 y multiplicado por 2).

5. Dominio y Rango

• Definición:
  • Dominio: Es el conjunto de todos los posibles valores de la variable independiente (x) para los cuales la función está definida.
  • Rango: Es el conjunto de todos los posibles valores de la variable dependiente (y) que la función puede tomar.
• Ejemplo 1:
  • Función: f(x)=x².
  • Dominio: Todos los números reales (R).
  • Rango: y≥0, porque x² nunca es negativo.

6. Funciones Explícitas e Implícitas

• Función Explícita: Es una función donde la variable dependiente está expresada claramente en términos de la variable independiente, por ejemplo, y = f(x).
  • Ejemplo 1: y=2x+3.
  • Ejemplo 2: y=x²+4x−5.
• Función Implícita: Es una función donde la relación entre las variables no está resuelta en términos de una sola variable, por ejemplo, x² + y² = 1.
  • Ejemplo 1: x²+y²=25(Ecuación de un círculo).
  • Ejemplo 2: xy+y²=10.

7. Notación de Intervalos

• Intervalos Abiertos: No incluyen los extremos del intervalo. Se denotan como (a, b).
• Intervalos Cerrados: Incluyen los extremos del intervalo. Se denotan como [a, b].
• Intervalos Semiabiertos/Semicerrados: Incluyen solo uno de los extremos. Se denotan como [a, b) o (a, b].

---

Representaciones de una Función

• Verbal: Se describe en palabras cómo se relacionan las variables. Ejemplo: “La función suma 3 a cualquier número dado.”
• Algebraica: Se expresa con una ecuación matemática. Ejemplo: f(x) = x + 3.
• Explícita: Se muestra de forma que la variable dependiente está aislada. Ejemplo: y = 2x + 1.
• Implícita: La relación entre las variables no está aislada. Ejemplo: x² + y² = 25.
• Tabular: Se presenta en una tabla que muestra los valores de entrada (x) y los correspondientes valores de salida (y).
• Gráfica: Se representa visualmente en un sistema de coordenadas cartesianas, donde el eje horizontal representa la variable independiente y el eje vertical la dependiente.

Tipos de Funciones Algebraicas

• Constante: Una función que siempre da el mismo valor sin importar el valor de la variable independiente. Ejemplo: f(x) = 5.
• Lineal: Una función cuya gráfica es una línea recta. Ejemplo: f(x) = 2x + 3.
• Cuadrática: Una función de segundo grado cuya gráfica es una parábola. Ejemplo: f(x) = x² – 4x + 4.
• Cúbica: Una función de tercer grado. Ejemplo: f(x) = x³ – 3x² + 2.
• Polinomial: Una función que es una suma de términos de la forma axⁿ, donde n es un número entero no negativo. Ejemplo: f(x) = x⁴ – 3x³ + x – 5.
• Racional: Una función que es el cociente de dos polinomios. Ejemplo: f(x) = 1/(x-2).
• Valor Absoluto: Una función que toma el valor absoluto de la variable independiente. Ejemplo: f(x) = |x|.
• Radical: Una función que involucra una raíz. Ejemplo: f(x) = √x.

Funciones Trascendentes

• Exponenciales: Funciones en las que la variable independiente aparece como exponente. Ejemplo: f(x) = e^x.
• Logarítmicas: La inversa de las funciones exponenciales. Ejemplo: f(x) = log(x).
• Trigonométricas: Funciones basadas en relaciones trigonométricas como seno, coseno y tangente. Ejemplo: f(x) = sin(x).