Fases y problemas del proceso estadístico
Podemos distinguir tres fases en el proceso estadístico:
- Muestreo: selección de la muestra que se analizará.
- Estadística Descriptiva: análisis particular de los datos de la muestra seleccionada.
- Inferencia Estadística: estudio de la posible generalización de los resultados obtenidos en la muestra al global de la población
Población: es el objeto del estudio.
Muestra: Sobre la población que se va a estudiar se toma un cierto carácter o rasgo que dará lugar a una variable, denótese por X, y que la población suele ser demasiado grande. Ello nos obliga a contentarnos con estudiar el carácter o rasgo sobre un subconjunto de n individuos de la población. La letra n queda reservada para denotar el tamaño de muestra.
En un sentido muy amplio, la Estadística Descriptiva es la parte o fase de la Estadística dedicada a la descripción de un conjunto de n datos.
En estadística, un censo es el proceso de recopilación de datos que abarca a todos los elementos o individuos de una población completa. Su objetivo es obtener información exhaustiva y detallada sobre características específicas de dicha población, sin necesidad de usar una muestra.
Ejemplo: Un censo nacional de población recoge datos de todos los habitantes de un país, como edad, género, ocupación y nivel educativo.
Parámetro: Es una medida numérica que describe una característica de toda la POBLACIÓN. Es un valor fijo, aunque generalmente desconocido, como la media o proporción poblacional.
Ejemplo: El promedio de edad de todos los estudiantes de una universidad.
Estadístico: Es una medida numérica que describe una característica de una MUESTRA de la población. Se utiliza como una estimación del parámetro poblacional.
Ejemplo: El promedio de edad de un grupo de 100 estudiantes seleccionados aleatoriamente de la universidad.
Clasificación de las técnicas de muestreo:
Muestreos Probabilísticos
Son aquellos en los que todos los elementos de la población tienen una probabilidad conocida y distinta de cero de ser seleccionados.
a) Aleatorio Simple
- Definición: Todos los elementos de la población tienen la misma probabilidad de ser seleccionados.
- Ejemplo: Una universidad quiere conocer la opinión de sus estudiantes sobre un nuevo programa académico. De una lista de 1,000 estudiantes, selecciona 100 al azar usando un generador de números aleatorios.
b) Sistemático
- Definición: Se selecciona un elemento cada cierto intervalo (k) a partir de un punto inicial aleatorio.
- Ejemplo: En una fábrica con 500 empleados, se elige al primer empleado al azar y luego a cada 10° empleado de la lista para un estudio sobre condiciones laborales.
c) Estratificado
- Definición: La población se divide en estratos (grupos homogéneos), y se selecciona una muestra aleatoria de cada estrato.
- Ejemplo: Un banco desea conocer la satisfacción de sus clientes en diferentes rangos de edad (18-30, 31-50, y 51+). Divide su base de datos en estos grupos y selecciona 50 clientes al azar de cada grupo.
d) Por Conglomerado
- Definición: La población se divide en conglomerados (grupos heterogéneos), y se selecciona aleatoriamente algunos conglomerados para estudiar todos sus elementos o tomar una muestra en ellos.
- Ejemplo: Una empresa de alimentos quiere evaluar la calidad de sus productos en supermercados. Divide la ciudad en sectores, selecciona 5 sectores al azar y estudia todos los supermercados dentro de esos sectores.
Muestreos No Probabilísticos
Son aquellos en los que no todos los elementos tienen la misma probabilidad de ser seleccionados.
a) Por Conveniencia
- Definición: Se seleccionan los elementos que son más accesibles o fáciles de obtener.
- Ejemplo: Un investigador entrevista a las primeras 20 personas que encuentra en una plaza comercial para saber sus preferencias sobre un producto.
b) Por Juicio o Criterio
- Definición: El investigador selecciona a los elementos que considera más representativos de la población.
- Ejemplo: Para evaluar el impacto de una reforma educativa, un experto selecciona a 10 escuelas que considera ejemplares según su criterio.
c) Por Bola de Nieve
- Definición: Se selecciona a un grupo inicial de participantes, quienes a su vez invitan a más personas, creando una «bola de nieve».
- Ejemplo: En un estudio sobre personas con enfermedades raras, se contacta a 3 pacientes que, a su vez, refieren a otros con la misma condición.
d) Por Cuotas
- Definición: Se selecciona una muestra que cumpla con ciertas características específicas.
- Ejemplo: Una encuesta busca 50 hombres y 50 mujeres mayores de 25 años. Se seleccionan de manera no aleatoria, pero cumpliendo la cuota.
El proceso del diseño de una muestra consta de varias etapas clave, que incluyen la identificación del tipo de variable, el cálculo del tamaño de la muestra y la selección de la técnica de muestreo. Aquí se explica cada uno de estos elementos:
1. Tipo de Variable
Determinar el tipo de variable es esencial para definir cómo se medirán los datos y qué métodos estadísticos se aplicarán.
- Variables Cualitativas: Describen cualidades o categorías (e.g., género, estado civil, tipo de producto).
- Ejemplo: «¿Cuál es tu género?» (Opciones: Masculino/Femenino/No binario).
- Variables Cuantitativas: Miden cantidades y son numéricas.
- Discretas: Toman valores específicos (e.g., número de hijos, cantidad de autos).
- Continuas: Pueden tomar cualquier valor dentro de un rango (e.g., peso, altura, ingresos).
- Ejemplo: «¿Cuánto pesas?» (Continuo, en kilogramos).
El tipo de variable influye en el diseño del cuestionario y en los métodos estadísticos para analizar los datos.
2. Tamaño de la Muestra
El tamaño de la muestra depende de:
- Tamaño de la población: Número total de elementos en la población (e.g., 5,000 estudiantes).
- Nivel de confianza: Probabilidad de que los resultados reflejen la realidad de la población (e.g., 95%).
- Margen de error: Tolerancia al error en los resultados (e.g., ±5%).
- Proporción esperada (p): Suposición inicial de la distribución de la característica de interés (e.g., 50% si no se conoce).
Fórmula para Tamaño de Muestra (para población infinita o desconocida):
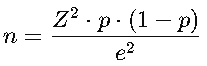
Donde:
- Z: Valor de Z-score según el nivel de confianza (1.96 para 95%).
- p: Proporción esperada (e.g., 0.5).
- e: Margen de error (e.g., 0.05).
Ajuste para Población Finita:
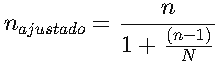
Donde N es el tamaño de la población.
3. Técnica de Muestreo
La técnica seleccionada depende de los objetivos de la investigación y las características de la población.
a) Muestreo Probabilístico (cuando se busca representatividad):
- Aleatorio Simple: Todos los elementos tienen la misma probabilidad de ser seleccionados.
- Sistemático: Se selecciona cada k-ésimo elemento a partir de un punto inicial aleatorio.
- Estratificado: La población se divide en grupos homogéneos y se selecciona una muestra de cada grupo.
- Por Conglomerado: Se divide la población en grupos heterogéneos y se seleccionan algunos grupos al azar.
b) Muestreo No Probabilístico (cuando no se puede asegurar representatividad):
- Conveniencia: Se seleccionan elementos accesibles o fáciles de contactar.
- Juicio: El investigador elige elementos que considera representativos.
- Bola de Nieve: Los participantes iniciales refieren a otros.
- Cuotas: Se establece una cuota por característica y se seleccionan elementos hasta completarla.
Ejemplo
Objetivo: Encuestar a estudiantes de una universidad sobre sus hábitos de estudio.
- Tipo de Variable:
- Variable cualitativa: «¿Prefieres estudiar solo o en grupo?».
- Variable cuantitativa: «¿Cuántas horas estudias al día?».
- Tamaño de la Muestra:
- Población: 10,000 estudiantes.
- Nivel de confianza: 95% (Z=1.96Z = 1.96Z=1.96).
- Margen de error: ±5% (e=0.05e = 0.05e=0.05).
- Proporción esperada: 50% (p=0.5p = 0.5p=0.5).
- Técnica de Muestreo:
- Estratificado: Dividir la población por carrera y seleccionar proporcionalmente estudiantes de cada carrera.