Operaciones Básicas entre Funciones

Definición
Una función f es una regla de correspondencia que asocia a cada objeto x en un conjunto —denominado dominio— un solo valor f (x) de un segundo conjunto. El conjunto de todos los valores así obtenidos se denomina rango de la función. (Véase la siguiente figura).

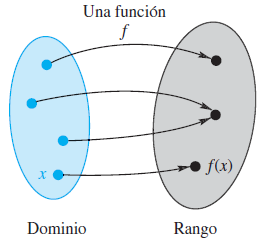
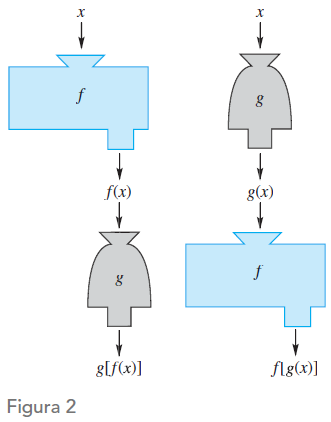
Piense en una función como una máquina que toma como entrada un valor x y produce una salida f (x). (Véase la figura 2). Cada valor de entrada se hace corresponder con un solo valor de salida. No obstante, puede suceder que diferentes valores de entrada den el mismo valor de salida.

Notación funcional Una sola letra como f (o g o F) se utiliza para nombrar una función. Entonces f (x), que se lee “f de x” o “f en x”, denota el valor que f asigna a x. Por lo tanto, si f (x) = x3 – 4, entonces

---

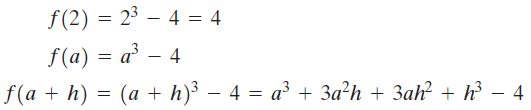
Al igual que dos números a y b pueden sumarse para producir un nuevo número a + b, también dos funciones f y g pueden sumarse para producir una nueva función f + g.

1. Suma de Funciones

Definición: La suma de dos funciones f(x) y g(x) es una nueva función h(x) que se obtiene sumando los valores de f(x) y g(x) para cada valor de x.

Expresión Matemática:
(f + g)(x) = f(x) + g(x)

Ejemplo: Si f(x) = 2x y g(x) = 3x + 1, entonces (f + g)(x) = 2x + 3x + 1 = 5x + 1.

2. Resta de Funciones

Definición: La resta de dos funciones f(x) y g(x) es una nueva función h(x) que se obtiene restando los valores de g(x) de los valores de f(x) para cada valor de x.

Expresión Matemática:
(f – g)(x) = f(x) – g(x)

Ejemplo: Si f(x) = 4x² y g(x) = 2x, entonces (f – g)(x) = 4x² – 2x.

3. Producto de Funciones

Definición: El producto de dos funciones f(x) y g(x) es una nueva función h(x) que se obtiene multiplicando los valores de f(x) y g(x) para cada valor de x.

Expresión Matemática:
(f · g)(x) = f(x) · g(x)

Ejemplo: Si f(x) = x y g(x) = x + 2, entonces (f · g)(x) = x · (x + 2) = x² + 2x.

4. Cociente de Funciones

Definición: El cociente de dos funciones f(x) y g(x) es una nueva función h(x) que se obtiene dividiendo los valores de f(x) por los valores de g(x) para cada valor de x, siempre que g(x) ≠ 0.

Expresión Matemática:
(f/g)(x) = f(x)/g(x)

Ejemplo: Si f(x) = x² y g(x) = x + 1, entonces (f/g)(x) = x² / (x + 1).

5. Composición de Funciones

Definición: La composición de dos funciones f(x) y g(x) es una nueva función h(x) que se obtiene aplicando g(x) primero y luego f(x) al resultado de g(x).

Expresión Matemática:
(f ∘ g)(x) = f(g(x))

Ejemplo: Si f(x) = 2x y g(x) = x² + 1, entonces (f ∘ g)(x) = f(g(x)) = 2(x² + 1) = 2x² + 2.

Al principio, le pedimos que pensase en una función como una máquina. Que recibe x como entrada, trabaja sobre x y produce f (x) como salida. Con frecuencia, dos máquinas se ponen una tras otra para producir una máquina más compleja; del mismo modo, dos funciones f y g (véase la figura 2). Si f actúa sobre x para producir f (x) y luego g actúa sobre f (x) para producir g(f (x)), decimos que hemos compuesto g con f. La función resultante, llamada composición de g con f, se denota con g ° f. Así,

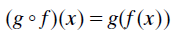
En nuestros ejemplos anteriores teníamos f (x) = (x – 3) y g(x) = √x. Podemos
componer estas funciones de dos maneras:

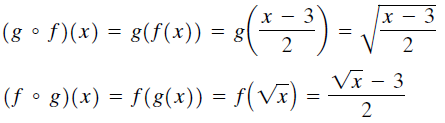
Enseguida notamos que g ° f no es igual a f ° g. Por lo tanto, decimos que la composición de funciones no es conmutativa.

Concepto de Condición Inicial en una Función

La condición inicial en una función se refiere al valor de la función y, posiblemente, sus derivadas en un punto específico, que se utiliza para determinar una solución única en problemas donde hay una familia de soluciones posibles. En otras palabras, es un valor específico que se impone a una función para determinar su comportamiento completo.

Ejemplo de Condición Inicial: Si tienes una función f(x) que describe una ecuación diferencial, una condición inicial podría ser f(0) = 1, lo que significa que el valor de la función en x = 0 es 1. Esto ayuda a definir una única solución a la ecuación diferencial que satisface esta condición.

Las condiciones iniciales son esenciales en muchas aplicaciones, como en la física y la ingeniería, donde se necesitan para resolver ecuaciones diferenciales que modelan sistemas dinámicos.