Proceso de Construcción y Validación de un Modelo Matemático con Funciones

El desarrollo de un modelo matemático con funciones sigue un conjunto de pasos sistemáticos para representar y analizar un fenómeno del mundo real. Este proceso incluye:
1. Definición del Problema
- Se identifica el fenómeno o sistema que se quiere modelar.
- Se establecen los objetivos del modelo (predicción, optimización, simulación, etc.).
- Se delimitan las variables dependientes e independientes.
2. Formulación del Modelo Matemático
- Se seleccionan funciones adecuadas (lineales, cuadráticas, exponenciales, logarítmicas, etc.).
- Se establecen ecuaciones que describan el comportamiento del sistema.
- Se consideran restricciones y condiciones iniciales.
3. Implementación Computacional
- Se traduce el modelo a código en software matemático como MATLAB, Python (NumPy/SciPy), R, Mathematica o Excel.
- Se prueban los valores iniciales y se ajustan los parámetros.
4. Validación y Calibración
- Se compara el modelo con datos reales para verificar su precisión.
- Se utilizan técnicas estadísticas como error cuadrático medio (MSE), coeficiente de correlación, regresión, etc..
- Si el modelo no es preciso, se ajustan las funciones o se consideran otros enfoques.
5. Análisis e Interpretación de Resultados
- Se analiza la validez del modelo en diferentes escenarios.
- Se evalúa la sensibilidad del modelo a cambios en los parámetros.
- Se realiza una interpretación de los resultados para la toma de decisiones.
6. Optimización y Refinamiento
- Se hacen ajustes para mejorar la eficiencia del modelo.
- Se prueban modelos alternativos o combinaciones de funciones.
Aplicación de Software en Funciones
Los modelos matemáticos con funciones se implementan en diversos software para su análisis y simulación:
| Software | Aplicación |
|---|---|
| MATLAB | Modelado y simulación de sistemas dinámicos, análisis de ecuaciones diferenciales. |
| Python (NumPy, SciPy, SymPy, TensorFlow) | Ajuste de funciones, predicciones estadísticas, inteligencia artificial. |
| R | Modelos estadísticos, regresiones, análisis de datos. |
| Excel | Modelos sencillos con funciones matemáticas y gráficas. |
| Wolfram Mathematica | Manipulación simbólica de funciones, cálculos avanzados. |
| GeoGebra | Visualización gráfica de funciones matemáticas. |
Ejemplo: Modelo de Crecimiento Poblacional con Función Exponencial
Supongamos que la población de una ciudad crece de acuerdo con la función:
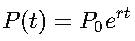
Donde:
- P(t) es la población en el tiempo ttt,
- P0 es la población inicial,
- r es la tasa de crecimiento,
- e es la base del logaritmo natural.
Este modelo puede ser implementado en Python:
Este modelo puede validarse comparando sus predicciones con datos reales y ajustando rrr para mejorar la precisión.
La construcción y validación de modelos matemáticos con funciones es esencial en diversas áreas como la economía, la ingeniería y la biología. Herramientas como Python, MATLAB y R facilitan su implementación, análisis y optimización.