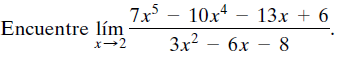Podríamos definir cálculo de esta manera:

El concepto de límite es primordial para muchos problemas en física, ingeniería y ciencias sociales. Básicamente, la pregunta es ésta: ¿qué le pasa con la función f(x) cuando x se acerca a alguna constante c? Existen variaciones de este tema, pero la idea básica es la misma en muchas circunstancias.
Podemos determinar áreas de rectángulos y triángulos por medio de fórmulas de geometría; pero, ¿qué hay de regiones con fronteras curvas, como un círculo? Arquímedes tuvo esta idea hace más de dos mil años. Imagine polígonos regulares inscritos en un círculo, como se muestra en la siguiente figura:
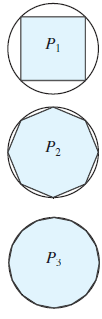
Arquímedes determinó el área de un polígono regular con n lados, y tomando el polígono cada vez con más lados fue capaz de aproximar el área de un círculo a cualquier nivel de precisión. En otras palabras, el área del círculo es el límite de las áreas de los polígonos inscritos cuando n (el número de lados del polígono) aumenta tanto como se quiera.
Considere la gráfica de la función y = f(x), para a <= x >= b. Si la gráfica es una línea recta, la longitud de la curva es fácil de determinar mediante la fórmula de la distancia. Sin embargo, ¿qué sucede si la gráfica es curvada? Podemos determinar una gran cantidad de puntos a lo largo de la curva y conectarlos con segmentos de recta, como se muestra en la siguiente figura:
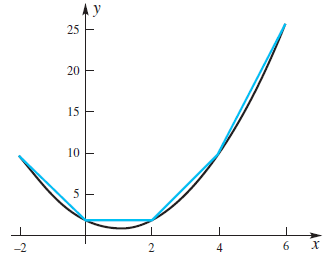
Observe que no está definida en x = 1, ¿cuando x se aproxima a 1, f (x) se está aproximando a algún número específico?
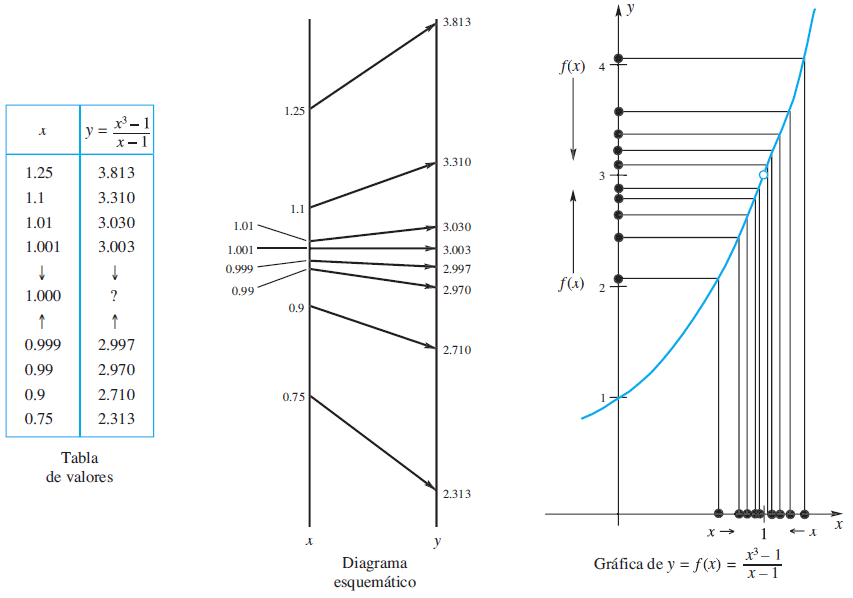
Toda la información que hemos reunido parece apuntar a la misma conclusión: f (x) se aproxima a 3 cuando x se aproxima a 1. En símbolos matemáticos, escribimos:
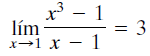
Esto se lee “el límite de (x3 – 1) / (x-1) cuando x tiende a 1 es 3”.
Como buenos algebristas (es decir, conociendo cómo se factoriza una diferencia de cubos), se tiene:
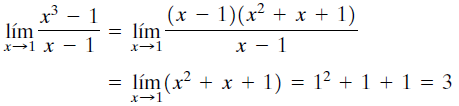
Límites laterales
Cuando una función da un salto, entonces el límite no existe en los puntos de salto. Para tales funciones, se introduce el concepto de límites laterales. El símbolo x→c+ significa que x se aproxima a c por la derecha, y x→c– significa que x se aproxima a c por la izquierda.


Ejemplos:
Ejemplo 1:
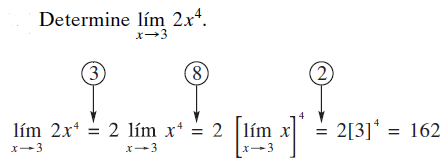
Ejemplo 2:
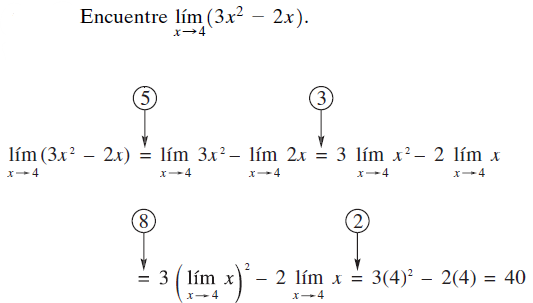
Ejemplo 3:


La demostración del teorema B se obtiene con base en aplicaciones repetidas del teorema A. Observe que el teorema B nos permite encontrar límites de funciones polinomiales y racionales con la simple sustitución de c por x en toda la expresión, siempre y cuando el denominador de la función racional no sea cero en c.
Ejemplo: