02 Cónicas 2da parte
Ecuaciones de la Elipse
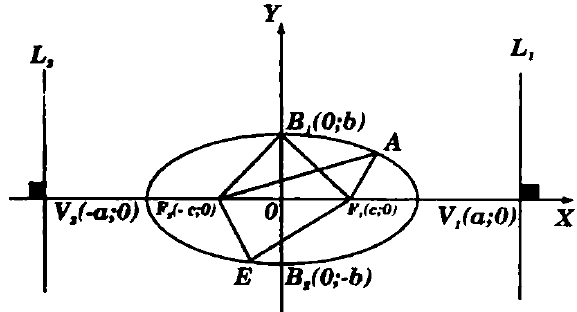
Dados dos puntos fijos F1 y F2 distintos, denominados Focos, se define la Elipse como el lugar geométrico del conjunto de puntos P(x;y) tales que la suma de distancias de P a los focos F1 y F2, es igual a una constante convencional 2a
(más…)03 Cónicas 3ra parte
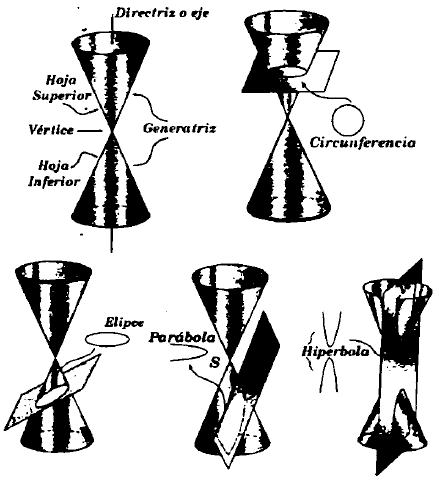
Las cónicas, abreviación de secciones cónicas, son curvas que se obtienen mediante la intersección de un cono circular recto con un plano.
Son Parábolas, cuando es inclinado de modo que es paralelo a solamente a una generatríz e intersecta a una rama del cono.
(más…)04 Conceptos de Funciones
Conceptos de Funciones
1. Variable
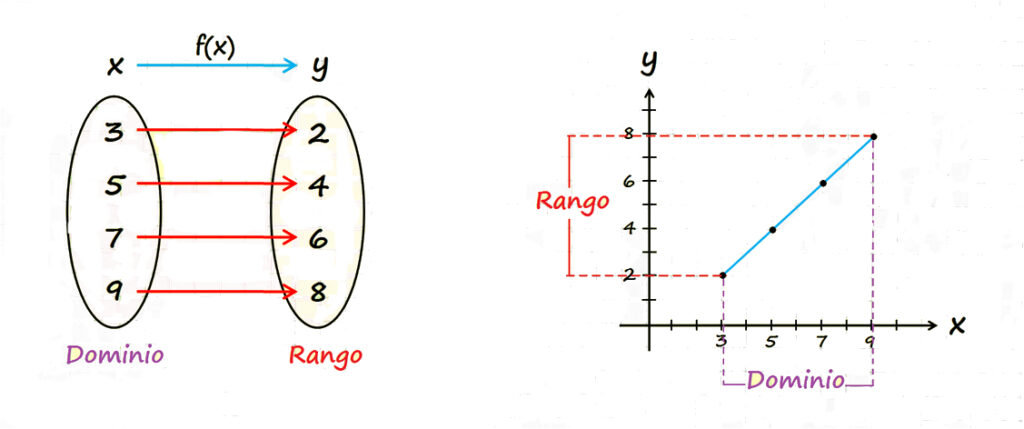
- Variable Independiente: Es la variable que se manipula o se elige libremente en una función. Generalmente, se representa por la letra x.
- Variable Dependiente: Es la variable que depende de la variable independiente. Su valor se determina a partir de la función aplicada a la variable independiente. Generalmente, se representa por la letra y o f(x).
2. Constante
Es un valor fijo que no cambia. En una función, una constante puede aparecer como un término independiente (por ejemplo, en f(x) = 2x + 3, el 3 es una constante).
05 Operaciones Básicas entre Funciones
Operaciones con Funciones
Operaciones Básicas entre Funciones
1. Suma de Funciones
Definición: La suma de dos funciones f(x) y g(x) es una nueva función h(x) que se obtiene sumando los valores de f(x) y g(x) para cada valor de x.
Expresión Matemática:
(f + g)(x) = f(x) + g(x)
Ejemplo: Si f(x) = 2x y g(x) = 3x + 1, entonces (f + g)(x) = 2x + 3x + 1 = 5x + 1.
(más…)06 Aplicaciones de Funciones
Aplicaciones de Funciones
Construcción y Validación de un Modelo Matemático con Funciones
(más…)La recta en el sistema cartesiano
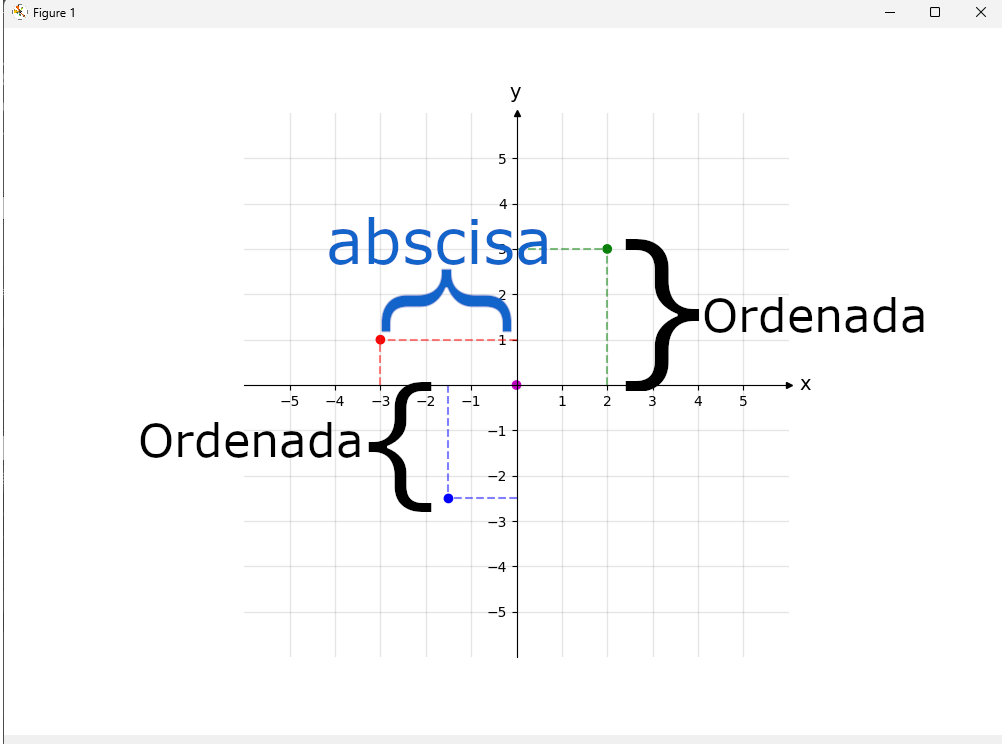
Las dos rectas que dan origen al plano cartesiano deben ser rectas numéricas, pues esa es la condición que hace posible encontrar las ubicaciones de los puntos cualesquiera en el plano. Esta ubicación es la base fundamental de muchos conocimientos comunes en la vida cotidiana, tales como la distancia entre puntos. Una recta numérica es una recta común en el que se estableció una correspondencia con los números reales
El plano cartesiano está formado por dos de estas rectas: Una responsable de la coordenada horizontal y otro responsable de la coordenada vertical. Es común el uso de las letras x para la primera y para la segunda, y los términos «coordenada x» y «coordinada»y».
Fuente: Partes de un plano cartesiano
https://planocartesiano.net/partes-de-un-plano-cartesiano
Geometría y Trigonometría
Perímetro, área y volumen
- Perímetro:
- Definición: Es la distancia total alrededor de una figura geométrica plana.
- Figuras comunes:
- Cuadrado: Todos los lados iguales.
- Rectángulo: Lados opuestos iguales.
- Círculo: Forma redonda, definida por su radio.
- Fórmulas:
- Cuadrado: 𝑃 = 4 × lado
- Rectángulo: 𝑃 = 2 × ( largo + ancho )
- Círculo: 𝑃 = 2 𝜋 𝑟(circunferencia)
- Área:
- Definición: Es la medida de la superficie que ocupa una figura geométrica plana.
- Figuras comunes:
- Cuadrado: Superficie con cuatro lados iguales.
- Rectángulo: Superficie con lados opuestos iguales.
- Círculo: Superficie circular definida por su radio.
- Fórmulas:
- Cuadrado: 𝐴 = lado 2
- Rectángulo: 𝐴 = largo × ancho
- Círculo: 𝐴 = 𝜋 𝑟 2
- Volumen:
- Definición: Es la cantidad de espacio que ocupa un cuerpo geométrico tridimensional.
- Cuerpos geométricos comunes:
- Cubo: Sólido con seis caras cuadradas iguales.
- Prisma rectangular (o paralelepípedo): Sólido con bases rectangulares.
- Esfera: Sólido perfectamente redondo, definido por su radio.
- Cilindro: Sólido con dos bases circulares y una superficie lateral.
- Fórmulas:
- Cubo: V=lado3
- Prisma rectangular: V=largo×ancho×alto
- Esfera: V=4⁄3 𝜋 𝑟 3
- Cilindro: V=𝜋 𝑟 2×altura
Sobre Límites
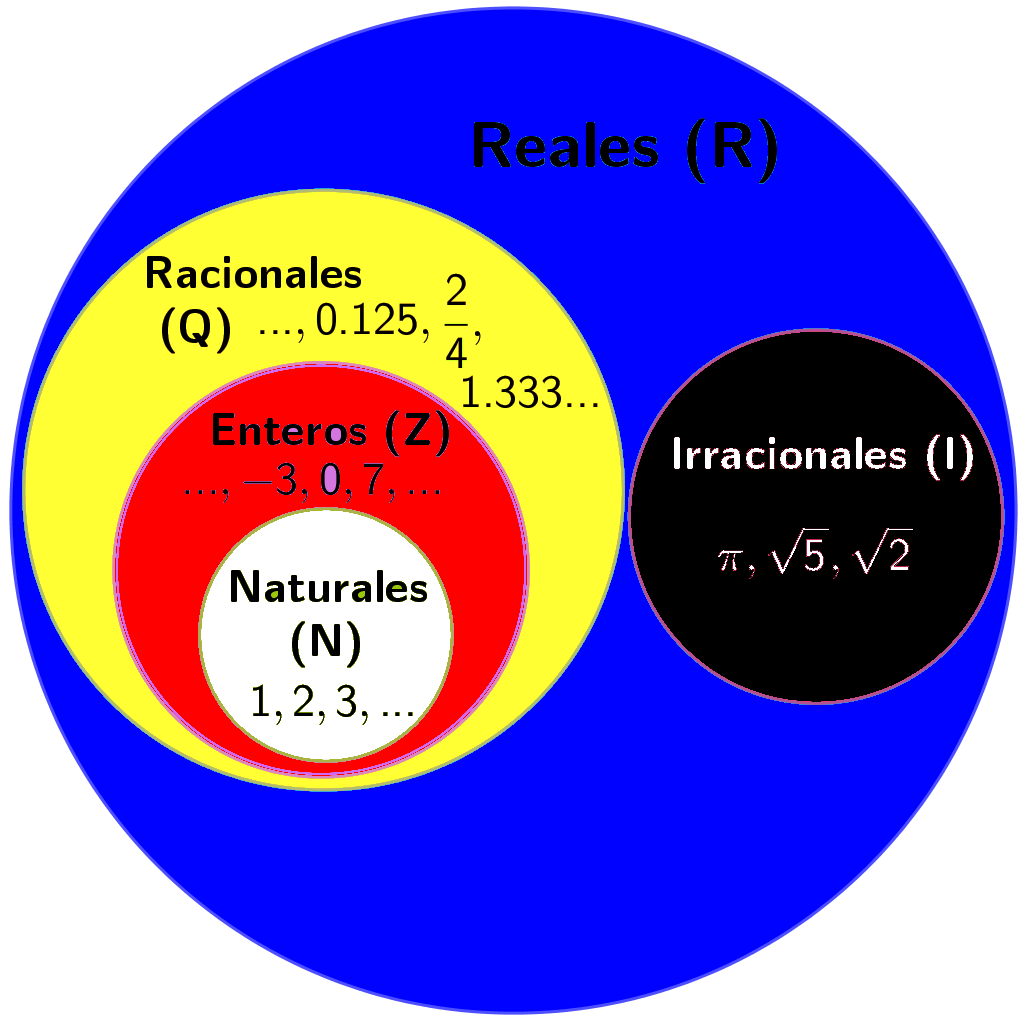
Los Numeros Naturales(N) son los enteros que representan existencias de lo que vemos, como 5 dedos, 2 ojos, 108 pétalos, etc, son números enteros positivos, pues en la naturaleza no hay fracciones ni negativos.
Los números enteros(Z), son los naturales y sus opuestos(los negativos) así como el cero(0).
en Los Números Racionales(Q), encontramos las fracciones, ya sean decimales o fraccionarias, positivas y negativas.
Los Números Irracionales(I) son aquellos que no representan una cantidad exacta, como se ejemplifica en la figura anterior.
Los Racionales(R) incluye a todos los anteriores
Ejercicios
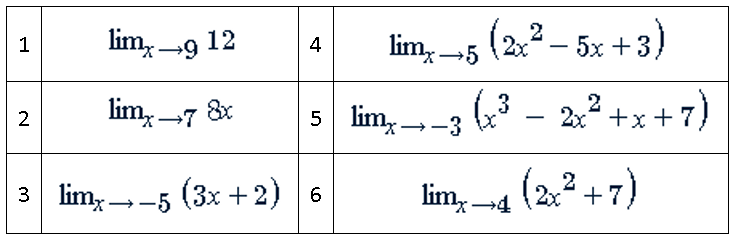
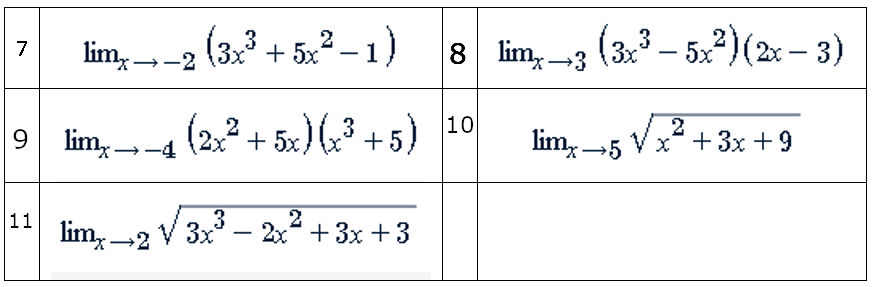
Metodologías de Desarrollo
La Metodología, (del griego metà “más allá”, odòs “camino” y logos “estudio”), hace referencia al conjunto de procedimientos basados en principios lógicos, utilizados para alcanzar una gama de objetivos que rigen en una investigación científica o en una exposición doctrinal.
(más…)